题目内容
在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y。
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围);
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由。
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围);
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由。
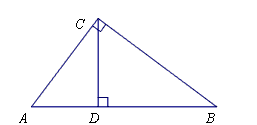
解:(1)∵AC=3,BC=4
∴AB=5
∵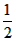 AC·BC=
AC·BC=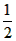 AB·CD,
AB·CD,
∴CD=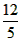 ,AD=
,AD=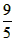 ;
;
(2)①当0<x≤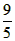 时
时
∵EF∥CD
∴△AEF∽△ADC
∴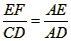
即EF=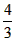 x
x
∴y=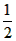 ·x·
·x·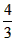 x=
x=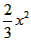
当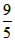 <x≤5时
<x≤5时
易得△BEF∽△BDC,同理可求EF=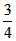 (5-x)
(5-x)
∴y=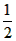 ·x·
·x·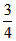 (5-x)=
(5-x)=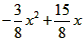 ≤
≤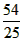
②当0<x≤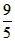 时,y随x的增大而增大,
时,y随x的增大而增大,
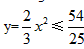 ,即当x=
,即当x=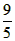 时,y最大值为
时,y最大值为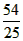
当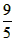 <x≤5时,
<x≤5时,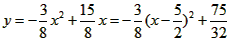
∵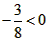
∴当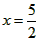 时,y的最大值为
时,y的最大值为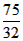
∵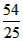 <
<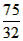
∴当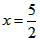 时,y的最大值为
时,y的最大值为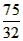 ;
;
(3)假设存在 当0<x≤5时,AF=6-x
∴0<6-x<3
∴3<x<6
∴3<x≤5
作FG⊥AB与点G 由△AFG∽△ACD可得
∴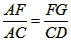 ,即FG=
,即FG=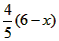
∴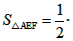 x·
x·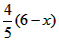 =
=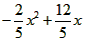
∴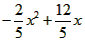 =3,即2x2-12x+5=0
=3,即2x2-12x+5=0
解之得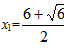 ,
,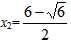
∵3<x1≤5
∴x1=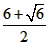 符合题意
符合题意
∵x2=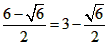 <3
<3
∴x2不合题意,应舍去
∴存在这样的直线EF,此时,x=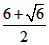 。
。
∴AB=5
∵
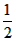 AC·BC=
AC·BC=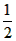 AB·CD,
AB·CD, ∴CD=
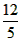 ,AD=
,AD=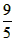 ;
;(2)①当0<x≤
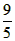 时
时 ∵EF∥CD
∴△AEF∽△ADC
∴
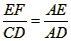
即EF=
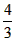 x
x∴y=
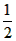 ·x·
·x·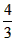 x=
x=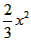
当
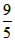 <x≤5时
<x≤5时易得△BEF∽△BDC,同理可求EF=
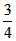 (5-x)
(5-x) ∴y=
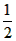 ·x·
·x·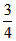 (5-x)=
(5-x)=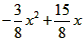 ≤
≤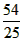
②当0<x≤
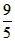 时,y随x的增大而增大,
时,y随x的增大而增大,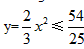 ,即当x=
,即当x=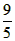 时,y最大值为
时,y最大值为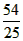
当
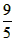 <x≤5时,
<x≤5时,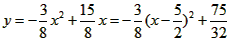
∵
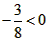
∴当
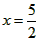 时,y的最大值为
时,y的最大值为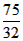
∵
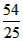 <
<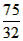
∴当
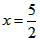 时,y的最大值为
时,y的最大值为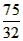 ;
;(3)假设存在 当0<x≤5时,AF=6-x
∴0<6-x<3
∴3<x<6
∴3<x≤5
作FG⊥AB与点G 由△AFG∽△ACD可得
∴
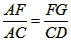 ,即FG=
,即FG=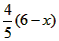
∴
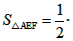 x·
x·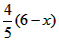 =
=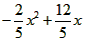
∴
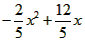 =3,即2x2-12x+5=0
=3,即2x2-12x+5=0 解之得
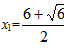 ,
,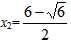
∵3<x1≤5
∴x1=
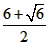 符合题意
符合题意 ∵x2=
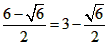 <3
<3 ∴x2不合题意,应舍去
∴存在这样的直线EF,此时,x=
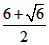 。
。
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于