Question

【题目】在平面直角坐标系中，抛物线的对称轴是直线．

（1）求抛物线的表达式；

（2）点， 在抛物线上，若，请直接写出的取值范围；

（3）设点为抛物线上的一个动点，当时，点关于轴的对称点都在直线的上方，求的取值范围．

Answer 1

【答案】（1）；（2）或；（3）

【解析】试题分析：（1）由抛物线的对称轴方程可求得m=1，从而可求得抛物线的表达式；

（2）将x=3代入抛物线的解析式，可求得y2=3，将y=3代入抛物线的解析式可求得x1=-1，x2=3，由抛物线的开口向下，可知当n<-1或n>3时，y1<y2；

（3）先根据题意画出点M关于y轴对称点M′的轨迹，然后根据点M关于y轴的对称点都在直线y=kx-4的上方，求出最大与最小两个关于k的方程，即可求得k的取值范围．

解：（1）∵抛物线的对称轴是,

∴,

∴,

∴．

（2）将x=3代入抛物线的解析式得y=32+2×3=3,

将y=3代入得：x2+2x=3,

解得：x1=1,x2=3.

∵a=1<0，

∴当n<1或n>3时,y1<y2.

（3） 由题意得抛物线,

关于轴对称的抛物线为.,

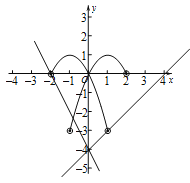
当,

当直线经过点时，

可得;

当,

当直线经过点时，

可得的取值范围是．