题目内容
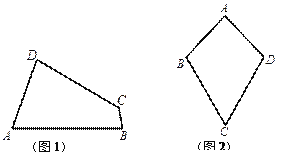
【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
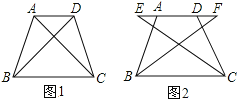
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
【答案】(1)证明见解析(2)BF=CE
【解析】试题分析:
(1)由∠ABC=∠DCB,AB=DC结合BC=CB即可证得:△ABC≌△DCB,从而可得AC=DB;
(2)由题意可得AE=DF,从而可得AF=DE,由AD∥BC结合∠ABC=∠DCB,易得∠BAD=∠CDA,再结合AB=DC即可证得△BAF≌△CDE,从而可得BF=CE.
试题解析:
(1)在△ABC和△DCB中,
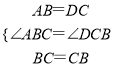 ,
,
∴△ABC≌△DCB(SAS),
∴AC=DB;
(2)BF=CE,理由如下:
由题意可得:AE=DF,
∴AF=DE,
∵AD∥BC,
∴∠BAD+∠ABC=180°,∠CDA+∠DCB=180°,
∵∠ABC=∠DCB,
∴∠BAD=∠CDA,
在△BAF和△CDE中,
 ,
,
∴△BAF≌△CDE(SAS),
∴BF=CE.

练习册系列答案
相关题目
【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 6:00 | 4小时 | 264千米 |
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 264千米 |