题目内容
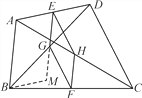
【题目】在四边形ABCD中，E、F分别是AD、BC的中点，G、H分别是BD、AC的中点，当AB、CD满足什么条件时，四边形EGFH是菱形？请证明你的结论．(提示：过点B作BM∥AD交EG的延长线于点M，证明EG//AB且EG=
AB)
【答案】见解析
【解析】试题分析：本题可根据菱形的定义来求解．E、G分别是AD，BD的中点，那么EG就是三角形ADB的中位线，同理，HF是三角形ABC的中位线，因此EG、HF同时平行且相等于AB，因此EG∥HF，EG=HF．因此四边形EHFG是平行四边形，E、H是AD，AC的中点，那么EH=
CD，要想证明EHFG是菱形，那么就需证明EG=EH，那么就需要AB、CD满足AB=CD的条件．
试题解析：当AB=CD时，四边形EGFH为菱形．
证明：过点B作BM∥AD交EG的延长线于点M，则∠DEG=∠GMB.∵G为BD的中点，∴DG=GB.
又∵∠DGE=∠BGM，∴△DGE≌△BGM，∴EG=GM，ED=BM.
∵E为AD的中点，∴AE=ED，∴BM∥AE，
∴四边形AEMB为平行四边形，
∴EM∥AB，
∴EG∥
AB，EG=
AB.
同理FH∥
CD，GF∥
CD，GF=
CD，
∴四边形EGFH为平行四边形．
∵AB=CD，∴GF=HF，
∴平行四边形EGHF是菱形．
练习册系列答案
相关题目
