��Ŀ����
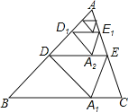
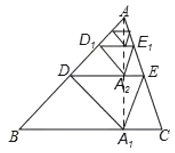
����Ŀ����ͼ������ABC���Ź�AB�е�D��ֱ���۵���ʹ��A����BC���ϵ�A1����Ϊ��1�β������ۺ�DE��BC�ľ����Ϊh1����ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2������Ϊ��2�β������ۺ�D1E1��BC�ľ����Ϊh2���������������ϲ�����ȥ����������2019�β�����õ����ۺ�D2018E2018����BC�ľ����Ϊh2019����h1��1����h2019��ֵΪ��____��
���𰸡�2��![]()
��������
�����е�����ʼ��۵������ʿɵ�DA��DA'��DB���Ӷ��ɵá�ADA'��2��B������۵������ʿɵá�ADA'��2��ADE���ɵá�ADE����B���̶��ж�DE��BC���ó�DE����ABC����λ�ߣ�֤��AA1��BC���õ�AA1��2�����h1��21��1��ͬ����h2��2![]() ��h3��2
��h3��2![]() ��
��![]() ��2
��2![]() ��������n�β�����õ����ۺ�Dn1En1��BC�ľ���hn��2
��������n�β�����õ����ۺ�Dn1En1��BC�ľ���hn��2![]() ��
��
�⣺���۵������ʿɵã�AA1��DE��DA��DA1��
�֡�D��AB�е㣬
��DA��DB��
��DB��DA1��
���BA1D����B��
���ADA1��2��B��
�֡ߡ�ADA1��2��ADE��
���ADE����B��
��DE��BC��
��AA1��BC��
��AA1��2h1��2��
��h1��21��1��
ͬ����h2��2![]() ��h3��2
��h3��2![]() ��
��![]() ��2
��2![]() ��
��
�ྭ����n�β�����õ����ۺ�Dn1En1��BC�ľ���hn��2![]() ��
��
��h2019��2![]() ��
��
�ʴ�Ϊ��2![]() .
.

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�