题目内容
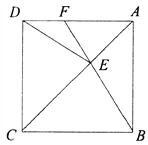
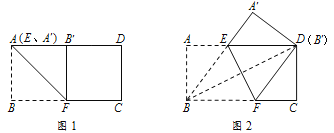
【题目】把一张矩形纸片ABCD按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F.
(1)试在图中连接BE,求证:四边形BFB′E是菱形;
(2)若AB=8,BC=16,求线段BF长能取到的整数值.

【答案】(1)证明见解析(2)8,9,10
【解析】试题分析:(1)连接BB′,由折叠知点B、B′关于EF对称,可知BE=B′E,BF=B′F,然后根据矩形的性质可证∠B′EF=B′FE,从而得到BE=B′E=B′F=BF,再由四条边都相等的四边形是菱形得证;
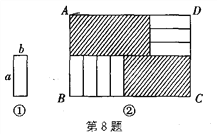
(2)如图1,当点E与点A重合时,四边形ABFB′是正方形,此时BF最小;如图2,当点B与点D重合时,BF最大,然后由勾股定理可求出范围,然后取整即可.
试题解析:(1)连接BB′.由折叠知点B、B′关于EF对称.
∴EF是线段BB′的垂直平分线.
∴BE=B′E,BF=B′F.
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠B′EF=∠BFE.
由折叠得B′FE=∠BFE.
∴∠B′EF=B′FE.
∴B′E=B′F.
∴BE=B′E=B′F=BF.
∴四边形BFB′E是菱形.
(2)如图1,当点E与点A重合时,四边形ABFB′是正方形,此时BF最小.
∵四边形ABFB′是正方形,
∴BF=AB=8,即BF最小为8.
如图2,当点B与点D重合时,BF最大.
设BF=![]() ,则CF=
,则CF=![]() ,DF=BF=
,DF=BF=![]() .
.
在Rt△CDF中,由勾股定理得CF2+CD2=DF2.
∴![]() =
=![]() ,解得
,解得![]() =10,即BF=10.
=10,即BF=10.
∴8≤BF≤10.
∴线段BF长能取到的整数值为8,9,10.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?