题目内容
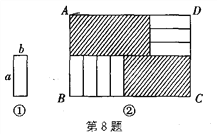
【题目】将7张如图①所示的长为a、宽为b（a>b）的小长方形纸片，按如图②所示的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示，设左上角与右下角的阴影部分的面积之差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a、b应满足( )
A. a＝
b B. a＝3b C. a＝
b D. a＝4b
【答案】A
【解析】试题解析：左上角阴影部分的长为AE，宽为AF=3b，右下角阴影部分的长为PC，宽为a，
∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC，
∴AE+a=4b+PC，即AE-PC=4b-a，
∴阴影部分面积之差S=AEAF-PCCG=3bAE-aPC=3b（PC+4b-a）-aPC=（3b-a）PC+12b2-3ab，
则3b-a=0，即a=3b．
故选B．
练习册系列答案
相关题目
【题目】在武汉教育电视台组织的一次汉字听写大赛中，10名参赛选手得分情况如下：
人数 | 3 | 4 | 2 | 1 |
分数 | 80 | 85 | 90 | 95 |
那么这10名选手所得分数的中位数和众数分别是（ ）
A. 85和85 B. 85.5和85 C. 85和4 D. 85.5和4
