题目内容
已知矩形ABCD中，对角线AC=10，周长为28，则矩形的面积为________．
48
分析：设长方形的长为x、宽为y，根据长方形的周长可以计算x+y的值，根据勾股定理即可列出关于x、y的方程式，即可求得x、y的值．
解答：长方形的长为x、宽为y，
矩形周长为28，则x+y=14，
且x2+y2=100，
解得x=8，y=6，
故矩形的面积为xy=6×8=48．
故答案为：48．
点评：本题考查了矩形面积的计算，长方形对边相等、对角线相等的性质，勾股定理在直角三角形中的运用，本题中根据x、y的关系式求x、y的值是解题的关键．
分析：设长方形的长为x、宽为y，根据长方形的周长可以计算x+y的值，根据勾股定理即可列出关于x、y的方程式，即可求得x、y的值．
解答：长方形的长为x、宽为y，
矩形周长为28，则x+y=14，
且x2+y2=100，
解得x=8，y=6，
故矩形的面积为xy=6×8=48．
故答案为：48．
点评：本题考查了矩形面积的计算，长方形对边相等、对角线相等的性质，勾股定理在直角三角形中的运用，本题中根据x、y的关系式求x、y的值是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
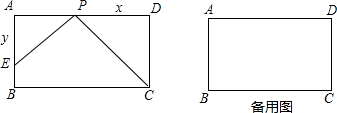
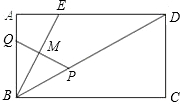，点Q从点B以每秒1个单位沿BA方向向点A运动，设运动时间为t秒，△BPQ的面积为S．
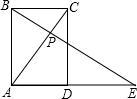如图，已知矩形ABCD中，BC=6，AB=8，延长AD到点E，使AE=15，连接BE交AC于点P．
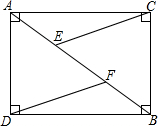如图：已知矩形ABCD中，CE∥DF．