题目内容
如图，点D、E分别是等边三角形△ABC边AB、BC上的点，且BD=CE，则∠AFE=________．
60°
分析：根据等边三角形的性质证明△BCE≌△ABD（SAS），根据全等三角形的对应角相等求得∠BAD=∠CBE，再根据∠CBE+∠ABE=60°，再根据∠AFE=∠BAD+∠ABE即可求解．
解答：在△BCE和△ABD中，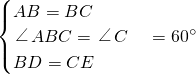
，
∴△BCE≌△ABD（SAS），
∴∠BAD=∠CBE（全等三角形的对应角相等）；
又∵∠CBE+∠ABE=60°，
∴∠BAD+∠ABE=60°，
在△ABF中，∠AFE=∠BAD+∠ABE=60°．
故答案是：60°．
点评：本题考查了等边三角形的性质、全等三角形的判定与性质．解答此题时，借助于三角形的外角性质（三角形的一个外角，等于与它不相邻的两个内角的和）来求的∠AFE的度数．
分析：根据等边三角形的性质证明△BCE≌△ABD（SAS），根据全等三角形的对应角相等求得∠BAD=∠CBE，再根据∠CBE+∠ABE=60°，再根据∠AFE=∠BAD+∠ABE即可求解．
解答：在△BCE和△ABD中，
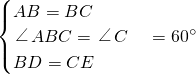，∴△BCE≌△ABD（SAS），
∴∠BAD=∠CBE（全等三角形的对应角相等）；
又∵∠CBE+∠ABE=60°，
∴∠BAD+∠ABE=60°，
在△ABF中，∠AFE=∠BAD+∠ABE=60°．
故答案是：60°．
点评：本题考查了等边三角形的性质、全等三角形的判定与性质．解答此题时，借助于三角形的外角性质（三角形的一个外角，等于与它不相邻的两个内角的和）来求的∠AFE的度数．
练习册系列答案
相关题目
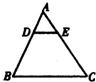17、如图，点D、E分别是△ABC边AB、AC上的点，且DE∥BC，BD=2AD，那么△ADE的周长：△ABC的周长=
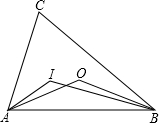（2013•武汉模拟）如图，点I和O分别是△ABC的内心和外心，则∠AIB和∠AOB的关系为（ ）
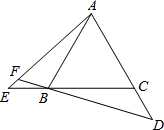如图，点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点，且BE=CD，DB延长线交于AE于点F，则∠AFB的度数是