Question

（1997•重庆）如图，以⊙O上一点O₁为圆心作圆和⊙O相交于A，B两点，过A作直线CD交⊙O于C，交⊙O₁于D．CB交⊙O₁于E，AB与CO交于F．
求证：（1）AC•BC=CF²+AF•BF；
      （2）∠CDB=∠CBD．

Answer 1

分析：（1）连接O₁A，O₁B，由圆的半径相等得到O₁A=O₁B，再利用等弦所对的劣弧相等得到两条弧相等，利用等弧所对的圆周角相等得到一对角相等，再利用同弧所对的圆周角相等得到另一对角相等，利用两对对应角相等的两三角形相似得到三角形AFC与三角形O₁BC相似，由相似得比例，等量代换即可得证；
（2）连接O₁D，则O₁D=O₁B=O₁A，利用等边对等角得到两对角相等，再由圆内接四边形的外角等于它的内对角得到一对角相等，等量代换即可得证．

解答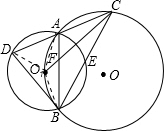：证明：（1）连接O₁A，O₁B，则O₁A=O₁B，
∴

O1A

=

O1B

，
∴∠ACF=∠BCF，
∵∠CAB=∠CO₁B，
∴△AFC∽△O₁BC，
∴

AC

O1C

=

CF

BC

，
∴AC•BC=O₁C•CF=（O₁F+CF）•CF=CF₂+O₁F•CF，
∵AF•BF=O₁F•CF，
∴AC•BC=CF₂+AF•BF；

（2）连接O₁D，则O₁D=O₁B=O₁A，
∴∠O₁DB=∠O₁BD，∠O₁DA=∠O₁AD，
∵∠O₁AD=∠CBO₁，
∴∠O₁DA=∠CBO₁，
∴∠O₁DA+∠O₁DB=∠O₁BD+∠CBO₁，即∠CDB=∠CBD．

点评：此题考查了相交两圆的性质，相似三角形的判定与性质，圆内接四边形的性质，以及圆周角定理，熟练掌握相交两圆的性质是解本题的关键．