题目内容
（1997•重庆）如图，PD切⊙O于A， |
| AB |
|
| BC |
40
40
度．分析：连接OC，根据切线的性质和圆心角定理计算即可．
解答：解：连接OC，
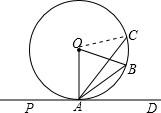∵∠CAP=120°，
∴∠CAD=60°，
∴∠COA=120°，
弧AC=120°
又∵AB弧=2BC，
∴AB弧=120×
=80°
∴∠BOA=80°，
∵OA=OB，
∴∠OAB=∠OBA=
=50°，
∵PD是⊙O切线，
∴∠OAD=90°，
∴∠DAB=90°-50°=40°，
故答案为：40．
∵∠CAP=120°，∴∠CAD=60°，
∴∠COA=120°，
弧AC=120°
又∵AB弧=2BC，
∴AB弧=120×
| 2 |
| 3 |
∴∠BOA=80°，
∵OA=OB，
∴∠OAB=∠OBA=
| 180°-80° |
| 2 |
∵PD是⊙O切线，
∴∠OAD=90°，
∴∠DAB=90°-50°=40°，
故答案为：40．
点评：本题考查了圆的切线的性质以及圆心角定理和圆心角所对弧的数量关系．
练习册系列答案
相关题目
（1997•重庆）如图．△ABC中，AB=AC，∠A=40°，∠ABC的平分线交AC于D，则∠BDC=
（1997•重庆）如图．两个同心圆，小圆的切线被大圆截得的部分为AB，两圆所围成的圆环面积是9π，则AB=
（1997•重庆）如图，Rt△ABC中，∠BAC=90°，过顶点A的直线DE∥BC，∠ABC，∠ACB的平分线分别交DE于E、D，若AC=6，BC=10，则DE=（ ）
（1997•重庆）如图，以⊙O上一点O1为圆心作圆和⊙O相交于A，B两点，过A作直线CD交⊙O于C，交⊙O1于D．CB交⊙O1于E，AB与CO交于F．