��Ŀ����
����Ŀ������ABC�У�AB=AC��
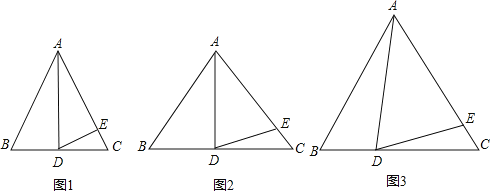
��1����ͼ1�������BAD=30����AD��BC�ϵĸߣ�AD=AE������EDC=
��2����ͼ2�������BAD=40����AD��BC�ϵĸߣ�AD=AE������EDC=
��3��˼����ͨ���������⣬�㷢����BAD����EDC֮����ʲô��ϵ������ʽ�ӱ�ʾ��
��4����ͼ3�����AD����BC�ϵĸߣ�AD=AE���Ƿ�����������ϵ�����У�����д��������˵�����ɣ�
���𰸡���1��15������2��20������3����EDC=![]() ��BAD����4���Գ���������������.
��BAD����4���Գ���������������.
��������
�����������1���������������ߺ�һ��������DAE=30��������ΪAD=AE��������ADE=��AED=75����������DEC=15����
��2��ͬ������֤��ADE=70����������DEC=20����
��3��ͨ����1����2����Ľ��ۿ�֪����BAD=2��EDC������EDC=![]() ��BAD����
��BAD����
��4������AD=AE��������ADE=��AED��������֪����֤��BAD+��B=2��EDC+��C����B=��C��������BAD=2��EDC��
�⣺��1��������ABC�У�AB=AC��AD��BC�ϵĸߣ�
���BAD=��CAD��
�ߡ�BAD=30����
���BAD=��CAD=30����
��AD=AE��
���ADE=��AED=75����
���EDC=15����
��2��������ABC�У�AB=AC��AD��BC�ϵĸߣ�
���BAD=��CAD��
�ߡ�BAD=40����
���BAD=��CAD=40����
��AD=AE��
���ADE=��AED=70����
���EDC=20����
��3����BAD=2��EDC������EDC=![]() ��BAD��
��BAD��
��4���Գ�������������
��AD=AE�����ADE=��AED��
���BAD+��B=��ADC=��ADE+��EDC=��AED+��EDC=����EDC+��C��+��EDC
=2��EDC+��C
����AB=AC��
���B=��C
���BAD=2��EDC��
�ʷֱ���15�㣬20�㣬��EDC=![]() ��BAD
��BAD