题目内容
【题目】数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如：如图①，若点A，B在数轴上分别对应的数为a，b(a<b)，则AB的长度可以表示为AB=b－a．
请你用以上知识解决问题：
如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动3个单位长度到达B点，然后向右移动5个单位长度到达C点．
（1）请你在图②的数轴上表示出A，B，C三点的位置．
（2）若点A以每秒1个单位长度的速度向左移动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动，设移动时间为t秒．
①当t=2时，求AB和AC的长度；
②试探究：在移动过程中，3AC－4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．
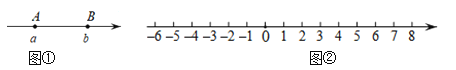
【答案】（1）详见解析；（2）①16；②在移动过程中，3AC﹣4AB的值不变
【解析】
（1）根据点的移动规律在数轴上作出对应的点即可；
（2）①当t=2时，先求出A、B、C点表示的数，然后利用定义求出AB、AC的长即可；
②先求出A、B、C点表示的数，然后利用定义求出AB、AC的长，代入3AC－4AB即可得到结论．
（1）A，B，C三点的位置如图所示：
．
（2）①当t=2时，A点表示的数为－4，B点表示的数为5，C点表示的数为12，∴AB=5－(－4)=9，AC=12－(－4)=16．
②3AC－4AB的值不变．
当移动时间为t秒时，A点表示的数为－t－2，B点表示的数为2t＋1，C点表示的数为3t＋6，则：AC=(3t＋6)－(－t－2)=4t＋8，AB=(2t＋1)－(－t－2)=3t＋3，∴3AC－4AB=3(4t＋8)－4(3t＋3)=12t＋24－12t－12=12．
即3AC﹣4AB的值为定值12，∴在移动过程中，3AC﹣4AB的值不变．
