题目内容
| |||||||||||||
答案:
解析:
解析:
(1) |
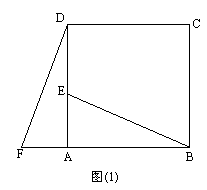
证明:∵E是AD的中点.∴AE= 又∵AD=AB,AF= ∵AD⊥AB,∴∠BAE=∠DAF= ∴△ABE≌△ADF |
(3) |
a.△ABE绕点A逆时针旋转 b.BE=DF,且BE⊥DF. 解析:由E是AD中点,AF= △ABE绕点A逆时针旋转 由(1)证明可知BE=DF,且BE⊥DF. |

练习册系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.