Question

【题目】如图，在平面直角坐标系中，OA=OB=，AB=．若点A坐标为（1，2），则点B的坐标为_____．

Answer 1

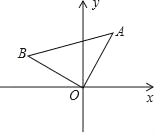
【答案】（﹣2，1）．

【解析】

作BN⊥x轴，AM⊥x轴，根据题意易证得△BNO≌△OMA，再根据全等三角形的性质可得NB=OM，NO=AM，又已知A点的坐标，即可得B点的坐标.

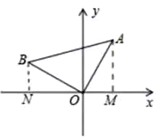
解：作BN⊥x轴，AM⊥x轴，

∵OA=OB=，AB=，

∴AO2+OB2=AB2，

∴∠BOA=90°，

∴∠BON+∠AOM=90°，

∵∠BON+∠NBO=90°，

∴∠AOM=∠NBO，

∵∠AOM=∠NBO，∠BNO=∠AMO，BO=OA，

∴△BNO≌△OMA，

∴NB=OM，NO=AM，

∵点A的坐标为（1,2），

∴点B的坐标为（-2,1）.

故答案为（-2,1）.