题目内容
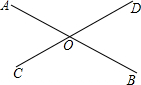
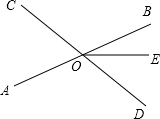
如图所示，直线AB，CD相交于点O，OE平分∠BOD，∠AOD-∠AOC=20°，求∠AOE的度数．
∵AB，CD相交于点O，
∴∠AOD+∠AOC=180°，
又∵∠AOD-∠AOC=20°，
∴∠AOD=∠AOC+20°，
∴2∠AOC+20°=180°，
∴∠AOC=80°，
由对顶角相等，得∠BOD=80°．
又∵OE平分∠BOD，
∴∠DOE=
∠BOD=
×80°=40°，
∴∠AOE=∠AOD+∠DOE=∠AOC+20°+40°=80°+20°+40°=140°．
∴∠AOD+∠AOC=180°，
又∵∠AOD-∠AOC=20°，
∴∠AOD=∠AOC+20°，
∴2∠AOC+20°=180°，
∴∠AOC=80°，
由对顶角相等，得∠BOD=80°．
又∵OE平分∠BOD，
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOE=∠AOD+∠DOE=∠AOC+20°+40°=80°+20°+40°=140°．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
