��Ŀ����
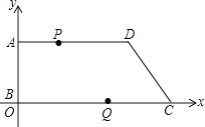
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬��B=45�㣬BC=10������A��AD��BC���ҵ�D�ڵ�A���Ҳ࣮��P�ӵ�A����������AD������ÿ��1����λ���ٶ��˶���ͬʱ��Q�ӵ�C����������CB������ÿ��2����λ���ٶ��˶������߶�QC��ȡ��E��ʹ��QE=2������PE�����P���˶�ʱ��Ϊt�룮
��1����PE��BC����BQ�ij���
��2�������Ƿ����t��ֵ��ʹ��A��B��E��PΪ������ı���Ϊƽ���ı��Σ������ڣ����t��ֵ���������ڣ���˵��������
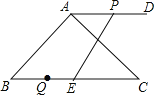
���𰸡�(1) BQ= ![]() ����2�����ڣ�t=4���������.
����2�����ڣ�t=4���������.
�����������������
(1)��AM��BC��M��PE��AC�ڵ�N������APN�͡�CEN�ǵ���ֱ�������Σ���CE�ij���PE�Ϻ���CM���ù���t��ʽ�ӱ�ʾ�����ɵõ�����t�ķ��̣��Ӷ���⣻
(2)����AP=BE���г�����t�ķ������.
���������
��1����AM��BC��M����ͼ��ʾ��
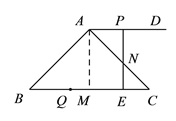
�ߡ�BAC=90�㣬��B=45�㣬���C=45��=��B��
��AB=AC����BM=CM����AM=![]() BC=5��
BC=5��
��AD��BC�����PAN=��C=45�㣬
��PE��BC����PE=AM=5��PE��AD��
���APN����CEN�ǵ���ֱ�������Σ�
��PN=AP=t��CE=NE=5-t��
��CE=CQ-QE=2t-2����5-t=2t-2��
��ã�t=![]() ��BQ=BC-CQ=10-2��
��BQ=BC-CQ=10-2��![]() =
= ![]() ��
��
��2�����ڣ�t=4���������£�
����A��B��E��PΪ������ı���Ϊƽ���ı��Σ�
��AP=BE��
��t=10-2t+2����ã�t=4��
������t��ֵ��ʹ��A��B��E��PΪ������ı���Ϊƽ���ı��Σ�t=4.

 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�