Question

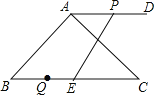
【题目】如图，AB是⊙O的直径，直线l与⊙O相切于点C，AE⊥l交直线l于点E、交⊙O于点F，BD⊥l交直线l于点D．

（1）求证：△AEC∽△CDB；

（2）求证：AE+EF=AB；

（3）若AC=8cm，BC=6cm，点P从点A出发沿线段AB向点B以2cm/s的速度运动，点Q从点B出发沿线段BC向点C以1cm/s的速度运动，两点同时出发，当点P运动到点B时，两点都停止运动．设运动时间为t秒，求当t为何值时，△BPQ为等腰三角形？

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）当t=或t=或t=时，△BPQ为等腰三角形．

【解析】试题分析：（1）、根据直角得出∠ACB=90°，即∠BCD+∠ACE=90°，根据AE⊥DE，BD⊥DE得出∠BCD=∠EAC，从而说明三角形相似；（2）、连接BF、OC根据DE为切线得出OC⊥DE，根据AE⊥DE，BD⊥DE得到OC∥BD∥AE，根据O为中点，得出OC为梯形的中位线，得到OC=，根据AB为直径得出∠BFE=90°，然后说明BDEF为矩形，得出BD=FE，即AE+EF=AE+BD，得到OC=，从而说明结论；（3）、首先根据题意求出AB和BP的长度，根据BP=BQ，BP=PQ，BQ=PQ三种情况求出t的值.

试题解析：（1）、∵AB是⊙O的直径 ∴∠ACB=90° ∴∠BCD+∠ACE=180°-∠ACB=90°

∵AE⊥DE，BD⊥DE ∴∠AEC=∠BDC=90° ∴∠ACE +∠EAC=90° ∴∠BCD =∠EAC ∴△AEC∽△CDB

（2）、连结BF、OC ∵DE切⊙O于点C ∴OC⊥DE

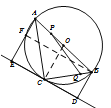
又∵AE⊥DE，BD⊥DE ∴OC∥BD∥AE又∵O是AB的中点 ∴OC是梯形ABDE的中位线

∴OC=∵AB是⊙O的直径 ∴∠AFB=90° ∴∠BFE=90°

又∵∠AED=∠BDE=90° ∴四边形BDEF是矩形

∴BD=FE ∴AE+EF=AE+BD ∴OC=∵OC= ∴AE+EF=AB

（3）、由题意可知：AP=2t，BQ=t，0＜t≤5 ∵∠ACB=90° ,AC="8,BC=6" ∴AB=∴BP=10-2t

当BP=BQ时 10-2t=t t=

②当PB=PQ时，过点P作PG⊥BC于点G ∵PB=PQ，PG⊥BC

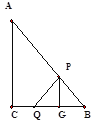
∴BG= = ，∠PGB=90°∴∠ACB=∠PGB =90° 又∵∠PBG=∠ABC ∴△BPG∽△BAC

∴∴

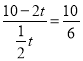
③当BQ=PQ时，过点Q作QH⊥AB于点H同理可求得：BH= = ，

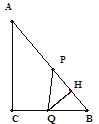
△QHB∽△ACB ∴∴∴t=

综上所述，当t=或t=或t=时，△BPQ为等腰三角形.