题目内容
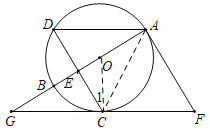
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接![]() ,
,![]() ,易证
,易证![]() 为等边三角形,可得
为等边三角形,可得![]() ,由等腰三角形的性质及角的和差关系可得∠1=30°,由于
,由等腰三角形的性质及角的和差关系可得∠1=30°,由于![]() 可得∠DCG=∠CDA=∠60°,即可求出∠OCG=90°,可得
可得∠DCG=∠CDA=∠60°,即可求出∠OCG=90°,可得![]() 与
与![]() 相切;(2)作
相切;(2)作![]() 于点
于点![]() .设
.设![]() ,则
,则![]() ,
,![]() .根据两组对边互相平行可证明四边形
.根据两组对边互相平行可证明四边形![]() 为平行四边形,由
为平行四边形,由![]() 可证四边形
可证四边形![]() 为菱形,由(1)得
为菱形,由(1)得![]() ,从而可求出
,从而可求出![]() 、
、![]() 的值,从而可知
的值,从而可知![]() 的长度,利用锐角三角函数的定义即可求出
的长度,利用锐角三角函数的定义即可求出![]() 的值.
的值.
(1)连接![]() ,
,![]() .
.
∵![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() 为等边三角形.
为等边三角形.
∴![]() ,∠DAE=∠EAC=30°,
,∠DAE=∠EAC=30°,
∵OA=OC,
∴∠OAC=∠OCA=30°,
∴∠1=∠DCA-∠OCA=30°,
∵![]() ,
,
∴∠DCG=∠CDA=∠60°,
∴∠OCG=∠DCG+∠1=60°+30°=90°,
∴![]() .
.
∴![]() 与
与![]() 相切.
相切.
(2)连接EF,作![]() 于点
于点![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
∵![]() 与
与![]() 相切,
相切,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() ,
,
∴四边形![]() 为菱形.
为菱形.
∴![]() ,
,![]() .
.
由(1)得![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴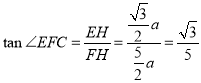 .
.

练习册系列答案
相关题目
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________