Question

（2013•海宁市模拟）如图，Rt△OAB的斜边OA在x轴上，点B在第一象限，OA：OB=5：4．边AB的垂直平分线分别交AB、x轴于点C、D，线段CD交反比例函数y=

3

x

的图象于点E．当BC=CE时，以DE为边的正方形的面积是（　　）

• A．

  25

  29

• B．1
• C．

  30

  29

• D．

  36

  29

Answer 1

分析：连结AE并且延长交OB于F点，连结BE，作FH⊥x轴于H，设OA=5x，则OB=4x，根据勾股定理计算出AB=3x，且A点坐标为（5x，0），根据垂直平分线的性质得CB=CA，EC⊥AB，EA=EB，DC=

1

2

OB=2x，而BC=CE，则EC=CA=CB=

3

2

x，所以△ABE为等腰直角三角形，同样得到△FBA为等腰直角三角形，则BF=BA=3x，EF=EA，得到OF=x，易证得Rt△OFH∽Rt△OAB，运用相似比可得到FH=

3

5

x，OH=

4

5

x，则F点坐标为（

4

5

x，

3

5

x），在求出AF的中点E的坐标（

29

10

x，

3

10

x），把E点坐标代入代入y=

3

x

求出x，则利用DE=DC-EC=2x-

3

2

x=

1

2

x求出DE，然后根据正方形面积公式计算即可．

解答：解：连结AE并且延长交OB于F点，连结BE，作FH⊥x轴于H，如图，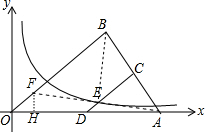
设OA=5x，则OB=4x，所以AB=

OA2-OB2

=3x，A点坐标为（5x，0），
∵边AB的垂直平分线分别交AB、x轴于点C、D，
∴CB=CA，EC⊥AB，EA=EB，DC=

1

2

OB=2x，
∵BC=CE，
∴EC=CA=CB=

3

2

x，
∴△ABE为等腰直角三角形，
∴BE⊥AE，∠EBA=45°，
而∠OBA=90°，
∴BE平分∠FBA，
∴△FBA为等腰直角三角形，
∴BF=BA=3x，EF=EA，
∴OF=OB-BF=x，
∵∠FOH=∠AOB，
∴Rt△OFH∽Rt△OAB，
∴

FH

AB

=

OH

OB

=

OF

OA

，即

FH

3x

=

OH

4x

=

x

5x

，
∴FH=

3

5

x，OH=

4

5

x，
∴F点坐标为（

4

5

x，

3

5

x），
∵E点为AF的中点，
∴E点坐标为（

29

10

x，

3

10

x），
把E（

29

10

x，

3

10

x）代入y=

3

x

得

29

10

x•

3

10

x=3，解得x=

10 29

29

，
∴DE=DC-EC=2x-

3

2

x=

1

2

x=

5 29

29

，
∴以DE为边的正方形的面积=DE²=（

5 29

29

）²=

25

29

．
故选A．

点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征、线段垂直平分线的性质和等腰直角三角形的判定与性质；熟练运用勾股定理和相似比进行几何计算．