题目内容
 (2013•海宁市模拟)如图,在正方形ABCD中,对角线AC,BD交于点O,∠ACB的平分线CE交BO于点E,过点B作BF⊥CE,垂足为F,交AC于点G,则
(2013•海宁市模拟)如图,在正方形ABCD中,对角线AC,BD交于点O,∠ACB的平分线CE交BO于点E,过点B作BF⊥CE,垂足为F,交AC于点G,则| BF |
| CE |
| 1 |
| 2 |
| 1 |
| 2 |
分析:利用正方形的性质,找出条件首先证得△BOG≌△COE,得出BG=CE,再证得△BCF≌△GCF,得出BF=GF=
BG,进一步利用等量代换求得问题.
| 1 |
| 2 |
解答:解:由ABCD是正方形,可知OB=OC.
∵∠BEF=∠OEC(对顶角相等)
∠BFE=∠COE=90°,
∴∠FBE=∠OCE,
又∵∠BOG=∠COE=90°,OC=OB,
∴△BOG≌△COE(ASA),
∴BG=CE,
又∵∠OCE=∠BCE,CF=CF,∠BFC=∠GFC=90°,
∴△BCF≌△GCF(SAS),
∴BF=FG=
BG,
∴
=
=
.
∵∠BEF=∠OEC(对顶角相等)
∠BFE=∠COE=90°,
∴∠FBE=∠OCE,
又∵∠BOG=∠COE=90°,OC=OB,
∴△BOG≌△COE(ASA),
∴BG=CE,
又∵∠OCE=∠BCE,CF=CF,∠BFC=∠GFC=90°,
∴△BCF≌△GCF(SAS),
∴BF=FG=
| 1 |
| 2 |
∴
| BF |
| CE |
| ||
| CE |
| 1 |
| 2 |
点评:此题主要考查正方形的性质,三角形全等的判定与性质等知识点.

练习册系列答案
相关题目
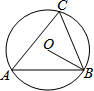 (2013•海宁市模拟)如图,⊙O是△ABC的外接圆,∠ABO=35°,则∠C的度数等于( )
(2013•海宁市模拟)如图,⊙O是△ABC的外接圆,∠ABO=35°,则∠C的度数等于( )