��Ŀ����
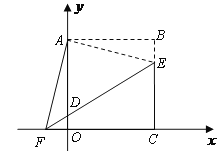
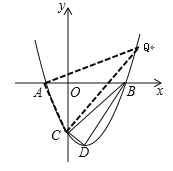
����Ŀ����ͼ��O������ԭ�㣬����A����1��0����������y=x2��bx��3��x�����һ������ΪB����y�ύ�ڵ�C���䶥��ΪD�㣮
��1����b��ֵ�Լ���D�����ꣻ
��2�����BCD�������
��3������BC��BD��CD����x�����Ƿ���ڵ�P��ʹ����A��C��PΪ��������������BCD���ƣ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
��4�������������Ƿ���ڵ�Q��ʹ����A��C��QΪ��������ACΪֱ�DZߵ�������Ϊֱ�������Σ������ڣ������Q�����ꣻ�������ڣ�˵�����ɣ�
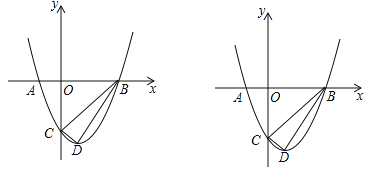
���𰸡���1��b=2 ��D��1��-4������2��3����3�����ڣ���0��0����9��0������4����0��-3������![]() ��-
��-![]() ������-1��0������
������-1��0������![]() ��
��![]() ����
����
��������
��1���ѵ�A����1��0������y=x2��bx��3�У����ݴ���ϵ�������ɵú�������ʽ�������䷽�����ɵö������ꣻ
��2������õ�B�����꣬Ȼ����S��BCD=S��BDM+S����OCDM-S��OBC��������ô𰸣�
��3���������������ε����ʣ�������������ó�AP�ij��������߶εĺͲ�ɵ�P�����꣮
��4�����������ľ��빫ʽ���ɶ�����ô𰸣�
�⣺��1����A��-1��0������y=x2-bx-3����1+b-3=0��
���b=2��
��y=x2-2x-3=��x-1��2-4��
��D��1��-4����
��2��
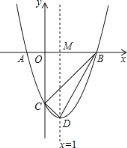
��C��0��-3����
��B��A����ֱ��x=1�Գƣ�
���B��3��0����
��ֱ��x=1��x���ڵ�M��
��OM=1��BM=3-1=2��DM=4��
��S��BCD=S��BDM+S����OCDM-S��OBC=![]() ��2��4+��
��2��4+��![]() ��3+4����1-
��3+4����1-![]() ��3��3=3��
��3��3=3��
��3����ͼ����y=0ʱ��x2-2x-3=0��
���x1=-1��x2=3����A��-1��0����B��3��0����D��1��-4����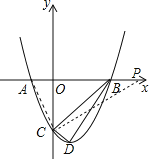
�ɹ��ɶ�������BC2=18��CD2=1+1=2��BD2=22+16=20��BC2+CD2=BD2����BCD=90����
�ٵ���APC�ס�DCBʱ��![]() ������
������![]() �����AP=1����P��0��0����
�����AP=1����P��0��0����
�ڵ���ACP�ס�DCBʱ��![]() ����
����![]() �����AP=10����P����9��0����
�����AP=10����P����9��0����
������������P�����꣨0��0����9��0����
��4����Q��������m��m 2-2m-3��
����QCA=90������AC2+CQ2=AQ2
�õ���32+��-1��2+��m 2-2m-3+3��2+m 2=��m+1��2+( m 2-2m-3)2��
���m=0��![]() ��
��
��Q��������0��-3����![]() ��-
��-![]() ��
��
����QAC=90������AC2+AQ2=CQ2
�õ���32+��-1��2 +��m+1��2+( m 2-2m-3)2=��m 2-2m-3+3��2+m 2��
���m=-1��![]() ��
��
��Q��������-1��0����![]() ��
��![]() ��
��
����������Q��������0��-3������![]() ��-
��-![]() ������-1��0������
������-1��0������![]() ��
��![]() ����
����

 �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�