Question

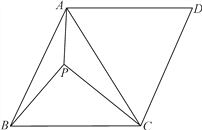
【题目】如图，在菱形中，，对角线平分角，点是内一点，连接、、，若，，，则菱形的面积等于_____________．

Answer 1

【答案】

【解析】分析：根据题意得出△ABC为等边三角形，以PA为边向△ABC外作一等边△APE(E点在AB边外)，连结BE，根据旋转的性质得出△BAE和△CAP全等，从而得出∠APB=150°，根据余弦定理得出△ABP的面积，从而得出△ABC的面积，最后根据菱形的面积等于两个△ABC的面积得出答案．

详解：∵AB=BC，∠B=60°， ∴△ABC为等边三角形，

设等边△ABC的边长为k，作BC边上的高AE,则BE=,由勾股定理得：AE=k，

∴ ，

以PA为边向△ABC外作一等边△APE(E点在AB边外)，连结BE，

可知：∠BAE+∠PAB=∠BAC=∠PAE=∠CAP+∠PAB=60°，

所以：∠BAE=∠CAP；AB=AC，AE=AP，因此，△BAE≌△CAP；则：BE=CP=10,

在△BPE中PE=6，PB=8，BE=1， ∴△BPE是直角三角形

∴∠APB=∠APE+∠BPE=60°+90°=150°,

在△ABP中由余弦定理得：=AB2=PA2+PB2－2×PA×PB×cos∠APB =100+48，

∴， ∴菱形的面积=()×2=