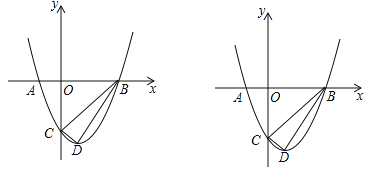题目内容
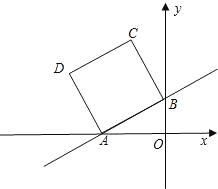
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
(1)求点A、B的坐标,并求边AB的长;
(2)求点C和点D的坐标;
(3)在x轴上找一点M,使△MDB的周长最小,请求出M点的坐标,并直接写出△MDB的周长最小值.
【答案】(1)A(﹣4,0),B(0,2);AB=2![]() ;(2)D(﹣6,4),C(﹣2,6);(3)M坐标为(﹣2,0),△MDB的周长为2
;(2)D(﹣6,4),C(﹣2,6);(3)M坐标为(﹣2,0),△MDB的周长为2![]() +6
+6![]() .
.
【解析】
(1)对于直线解析式,分别令x=0与y=0求出对应y与x的值,确定出A与B的坐标,得到OA与OB的长,利用勾股定理求出AB的长即可;
(2)过D作DE垂直于x轴,过C作CF垂直于y轴,根据四边形ABCD的正方形,得到四条边相等,四个角为直角,利用同角的余角相等得到三个角相等,利用AAS得到△EDA,△AOB以及△BFC全等,利用全等三角形的对应边相等得到DE=OA=BF=4,AE=OB=CF=2,进而求出OE与OF的长,即可确定出D与C的坐标;
(3)找出B关于y轴的对称点B′,连接DB′,交x轴于点M,此时BM+MD=DM+MB′=DB′最小,即△BDM周长最小,设直线DB′解析式为y=kx+b,把D与B′坐标代入求出k与b的值,确定出直线DB′解析式,令y=0求出x的值,确定出此时M的坐标即可.
解:(1)对于直线y=![]() x+2,
x+2,
令x=0,得到y=2;令y=0,得到x=﹣4,
∴A(﹣4,0),B(0,2),即OA=4,OB=2,
则AB=![]() =2
=2![]() ;
;
(2)过D作DE⊥x轴,过C作CF⊥y轴,
∵四边形ABCD为正方形,
∴AB=BC=AD,∠ABC=∠BAD=∠BFC=∠DEA=∠AOB=90°,
∵∠FBC+∠ABO=90°,∠ABO+∠BAO=90°,∠DAE+∠BAO=90°,
∴∠FBC=∠OAB=∠EDA,
∴△DEA≌△AOB≌△BFC(AAS),
∴AE=OB=CF=2,DE=OA=FB=4,
即OE=OA+AE=4+2=6,OF=OB+BF=2+4=6,
则D(﹣6,4),C(﹣2,6);
(3)如图所示,连接BD,找出B关于y轴的对称点B′,连接DB′,交x轴于点M,此时BM+MD=DM+MB′=DB′最小,即△BDM周长最小,
∵B(0,2),
∴B′(0,﹣2),
设直线DB′解析式为y=kx+b,
把D(﹣6,4),B′(0,﹣2)代入得:![]() ,
,
解得:k=﹣1,b=﹣2,
∴直线DB′解析式为y=﹣x﹣2,
令y=0,得到x=﹣2,
则M坐标为(﹣2,0),
此时△MDB的周长为2![]() +6
+6![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?