题目内容
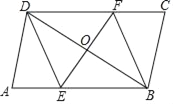
【题目】如图所示,平行四边形形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)请添加一个条件使四边形BEDF为菱形.
【答案】见解析
【解析】
(1)根据平行四边形的性质可得AB∥DC,OB=OD,由平行线的性质可得∠OBE=∠ODF,利用ASA判定△BOE≌△DOF,由全等三角形的性质可得EO=FO,根据对角线互相平分的四边形是平行四边形即可判定四边形BEDF是平行四边形;(2)添加EF⊥BD(本题添加的条件不唯一),根据对角线互相垂直的平行四边形为菱形即可判定平行四边形BEDF为菱形.
(1)∵四边形ABCD是平行四边形,O是BD的中点,
∴AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)EF⊥BD.
∵四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目