题目内容
【题目】如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=6,DF平分∠EDC交BC于F,DE⊥DC交AB于点E,连结EF.
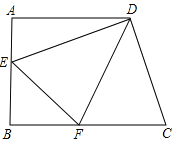
(1)证明:EF=CF
(2)当tan∠ADE =![]() 时,求EF的长.
时,求EF的长.
【答案】(1)证明见解析;(2)5.
【解析】
试题分析:(1)过D作DG⊥BC于G,由已知可得四边形ABGD为正方形,然后利用正方形的性质和已知条件证明△ADE≌△GDC,接着利用全等三角形的性质证明△EDF≌△CDF,
(2)由tan∠ADE=![]() ,根据已知条件可以求出AE=GC=2.设EF=x,则BF=8-CF=8-x,BE=4.在Rt△BEF中根据勾股定理即可求出x,也就求出了EF.
,根据已知条件可以求出AE=GC=2.设EF=x,则BF=8-CF=8-x,BE=4.在Rt△BEF中根据勾股定理即可求出x,也就求出了EF.
试题解析:(1)过D作DG⊥BC于G.
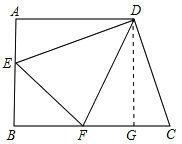
由已知可得四边形ABGD为正方形,
∵DE⊥DC.
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC.
又∵∠A=∠DGC且AD=GD,
∴△ADE≌△GDC,
∴DE=DC且AE=GC.
在△EDF和△CDF中
 ,
,
∴△EDF≌△CDF,
∴EF=CF;
(2)∵tan∠ADE=![]() ,
,
∴AE=GC=2.
∴BC=8,
BE=4,设CF=x,则BF=8-CF=8-x,
在Rt△BEF中,由勾股定理得:x2=(8-x)2+42,
解得x=5,
即EF=5.

练习册系列答案
相关题目