Question

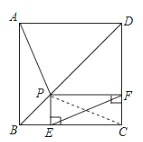
【题目】如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于E，PF⊥CD于F，连接EF，给出下列四个结论：①AP=EF,②△APD一定是等腰三角形，③∠PFE=∠BAP,④PD=EC.其中正确结论的序号是（ ）

A.①②④B.②④C.①②③D.①③④

Answer 1

【答案】D

【解析】

连接PC，根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°，然后利用“边角边”证明△ABP和△CBP全等，根据全等三角形对应边相等可得AP=PC，对应角相等可得∠BAP=∠BCP，再根据矩形的对角线相等可得EF=PC，对边相等可得PF=EC，再判断出△PDF是等腰直角三角形，然后根据等腰直角三角形的斜边等于直角边的倍解答即可．

如图，连接PC，在正方形ABCD中，∠ABP=∠CBP=45°，AB=CB，
∵在△ABP和△CBP中，

，

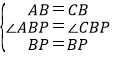∴△ABP≌△CBP（SAS），
∴AP=PC，∠BAP=∠BCP，
又∵PE⊥BC，PF⊥CD，
∴四边形PECF是矩形，
∴PC=EF，∠BCP=∠PFE，
∴AP=EF，∠PFE=∠BAP，故①③正确；
∵PF⊥CD，∠BDC=45°，
∴△PDF是等腰直角三角形，
∴PD=PF，
又∵矩形的对边PF=EC，
∴PD=EC，故④正确；
只有点P为BD的中点或PD=AD时，△APD是等腰三角形，故②错误；
综上所述，正确的结论有①③④．

故选：D.