题目内容
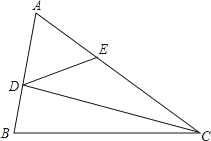
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
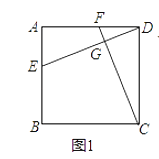
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;
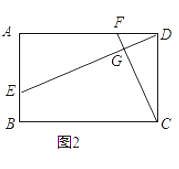
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
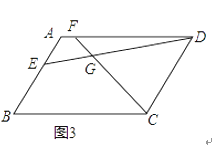
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)当∠B=∠EGF时,![]() 成立,证明见解析.
成立,证明见解析.
【解析】
(1)由四边形ABCD为正方形,利用正方形的性质得到一对角为直角,相等,且AD=DC,利用同角的余角相等得到一对角相等,利用AAS得到三角形ADE与三角形DCF全等,利用全等三角形对应边相等即可得证;
(2)由四边形ABCD为矩形,得到一对直角相等,利用同角的余角相等得到一对角相等,利用两对角相等的三角形相似得到三角形ADE与三角形DCF相似,利用相似三角形对应边成比例即可得证;
(3)当∠B=∠EGF时,![]() 成立,理由为:如图3,在AD的延长线上取点M,使CM=CF,利用平行线的性质,以及同角的补角相等得到三角形ADE与三角形DCM相似,利用相似三角形对应边成比例即可得证.
成立,理由为:如图3,在AD的延长线上取点M,使CM=CF,利用平行线的性质,以及同角的补角相等得到三角形ADE与三角形DCM相似,利用相似三角形对应边成比例即可得证.
(1)∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,
∴∠AED=∠CFD,
∴△ADE≌△DCF,
∴DE=CF
(2)∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,∠DCF+∠CFD=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴![]()
(3)解:当∠B=∠EGF时, ![]() 成立,
成立,
证明:如图3,在AD的延长线上取点M,使CM=CF,

则∠CMF=∠CFM,
∵AB∥CD,
∴∠A=∠CDM,
∵AD∥BC,
∴∠B+∠A=180°,
∵∠B=∠EGF,
∴∠EGF+∠A=180°,
∴∠AED=∠CFM=∠CMF,
∴△ADE∽△DCM,
∴ ![]() ,即
,即 ![]() .
.