题目内容
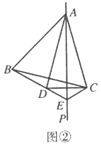
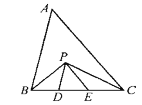
【题目】如图,在△ABC中.BC=5cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是______cm
【答案】5
【解析】
分别利用角平分线的性质和平行线的性质,求得△DBP和△ECP为等腰三角形,由等腰三角形的性质得BD=PD,CE=PE,那么△PDE的周长就转化为BC的长,即5cm.
解:∵BP、CP分别是∠ABC和∠ACB的平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠ACP=∠CPE,
∴∠PBD=∠BPD,∠PCE=∠CPE,
∴BD=PD,CE=PE,
∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm.
故答案为:5.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目