题目内容
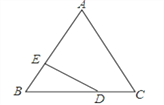
【题目】
是等边三角形，作直线
，点
关于直线的对称点为
，连接
，直线
交直线于点
，连接
．
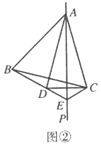
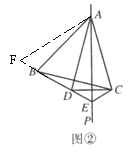
（1）如图①，求证：
；（提示：在BE上截取
，连接
．）
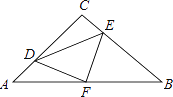
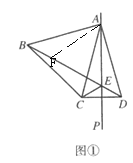
（2）如图②、图③，请直接写出线段，
，
之间的数量关系，不需要证明；
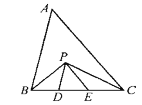
（3）在（1）、（2）的条件下，若
，则
__________．
【答案】（1）见解析；（2）图②中，CE+BE=AE，图③中，AE+BE=CE；（3）1.5或4.5
【解析】
（1）在BE上截取
，连接
，只要证明△AED≌△AFB，进而证出△AFE为等边三角形，得出CE+AE= BF+FE，即可解决问题；
（2）图②中，CE+BE=AE，延长EB到F，使BF=CE，连接，只要证明△ACE≌△AFB，进而证出△AFE为等边三角形，得出CE+BE= BF+BE，即可解决问题；图③中，AE+BE=CE，在EC上截取CF=BE，连接，只要证明△AEB≌△AFC，进而证出△AFE为等边三角形，得出AE+BE =CF+EF，即可解决问题；
（3）根据线段
，
，
，BD之间的数量关系分别列式计算即可解决问题．
（1）证明：在BE上截取，连接，
在等边△ABC中，
AC=AB，∠BAC=60°
由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，
设∠EAC=∠DAE=x．
∵AD=AC=AB，
∴∠D=∠ABD=
（180°-∠BAC-2x）=60°-x，
∴∠AEB=60-x+x=60°．
∵AC=AB，AC=AD，
∴AB=AD，
∴∠ABF=∠ADE，
∵，
∴△ABF≌△ADE，
∴AF=AE，BF=DE，
∴△AFE为等边三角形，
∴EF=AE，
∵AP是CD的垂直平分线，
∴CE=DE，
∴CE=DE=BF，
∴CE+AE= BF+FE =BE；
（2）图②中，CE+BE=AE，延长EB到F，使BF=CE，连接
在等边△ABC中，
AC=AB，∠BAC=60°
由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，
∴AB =AD，CE=DE，
∵AE =AE
∴△ACE≌△ADE，
∴∠ACE=∠ADE
∵AB =AD，
∴∠ABD=∠ADB
∴∠ABF=∠ADE=∠ACE
∵AB=AC，BF=CE，
∴△ACE≌△ABF，
∴AE=AF，∠BAF=∠CAE
∵∠BAC=∠BAE+∠CAE =60°
∴∠EAF=∠BAE+∠BAF =60°
∴△AFE为等边三角形，
∴EF=AE，
∴AE=BE+BF= BE+CE，即CE+BE=AE；
图③中，AE+BE=CE，在EC上截取CF=BE，连接，
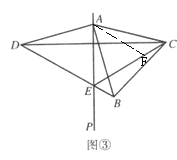
在等边△ABC中，
AC=AB，∠BAC=60°
由对称可知：AP是CD的垂直平分线，AC=AD，∠EAC=∠EAD，
∴AB =AD，CE=DE，
∵AE =AE
∴△ACE≌△ADE，
∴∠ACE=∠ADE
∵AB =AD，
∴∠ABD=∠ADB
∴∠ABD=∠ADE=∠ACE
∵AB=AC，BE=CF，
∴△ACF≌△ABE，
∴AE=AF，∠BAE=∠CAF
∵∠BAC=∠BAF+∠CAF =60°
∴∠EAF=∠BAF+∠BAE =60°
∴△AFE为等边三角形，
∴EF=AE，
∴CE =EF+CF= AE + BE，即AE+BE=CE；
（3）在（1）的条件下，若
，则AE=3，
∵CE+AE=BE，
∴BE-CE=3，
∵BD=BE+ED=BE+CE=6，
∴CE=1.5；
在（2）的条件下，若，则AE=3，因为图②中，CE+BE=AE，而BD=BE-DE=BE-CE，所以BD不可能等于2AE；
图③中，若，则AE=3，
∵AE+BE=CE，
∴CE-BE=3，
∵BD=BE+ED=BE+CE=6，
∴CE=4.5．
即CE=1.5或4.5．
