Question

【题目】在等腰中，，点是延长线上一点，连接，点是上一点，连接交于点，．

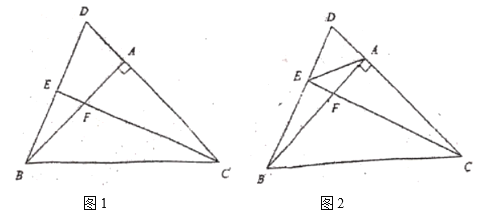
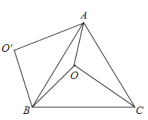
（1）如图1，当点是中点时，若，求的长；

（2）如图2，连接，求证：

Answer 1

【答案】（1）4-2

（2）见解析

【解析】

（1）只要证明Rt△BAD≌Rt△CAF（HL），推出∠DBA=∠ACF，因为∠EFB=∠AFC，推出∠BEF=∠FAC=90°，即可证明CB=CD=4解决问题；
（2）如图2中，作AM⊥BD于M，AN⊥EC于N．只要证明四边形AMEN是正方形，Rt△AMD≌Rt△ANF（HL）即可解决问题；

（1）解：如图1中，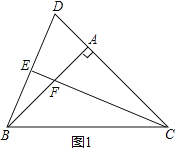

∵AB=AC，∠BAC=90°，BC=4，
∴AB=AC=2，
∵BD=CF，AB=AC，
∴Rt△BAD≌Rt△CAF（HL），
∴∠DBA=∠ACF，
∵∠EFB=∠AFC，
∴∠BEF=∠FAC=90°，
∴CE⊥BD，
∵BE=DE，
∴CB=CD=4，
∴AF=AD=CD-AC=4-2．
（2）证明：如图2中，作AM⊥BD于M，AN⊥EC于N．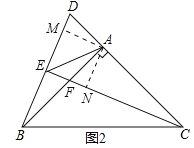

∵△BAD≌△CAF，AM⊥BD于M，AN⊥EC于N．
∴AM=AN（全等三角形对应边上的高相等），
∴∠AEM=∠AEN=45°，
∴AM=EM=EN=AN，
∴四边形AMEN是正方形，
∵AD=AF，AM=AN，
∴Rt△AMD≌Rt△ANF（HL），
∴DM=FN，
∴DE+EF=EM+DM+EN-FN=2EM，
∵AE=EM，
∴DE+EF=AE．