题目内容
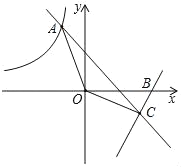
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边AC,BC上,
分别在边AC,BC上,![]() ,连接BD,点F,P,G分别为AB,BD,DE的中点.
,连接BD,点F,P,G分别为AB,BD,DE的中点.
(1)如图1中,线段PF与PG的数量关系是 ,位置关系是 ;
(2)若把△ CDE绕点C逆时针方向旋转到图2的位置,连接AD,BE,GF,判断△ FGP的形状,并说明理由;
(3)若把△ CDE绕点C在平面内自由旋转,AC=8,CD=3,请求出△FGP面积的最大值.

【答案】1)PF=PG PF⊥PG;(2)△FGP是等腰直角三角形,理由见解析;(3)S△PGF最大=![]() .
.
【解析】
(1)根据等腰三角形的性质和三角形的中位线定理解答即可;
(2)由旋转知,∠ACD=∠BCE,进一步证明△CAD≌△CBE,再利用全等三角形的判定和性质以及三角形中位线定理解答;
(3)由(2)知,△FGP是等腰直角三角形,PG=PF=![]() AD,PG最大时,△FGP面积最大,进而解答即可.
AD,PG最大时,△FGP面积最大,进而解答即可.
解(1)PF=PG PF⊥PG;
如图1,∵在△ABC中,AB=BC,点![]() ,
,![]() 分别在边AC,BC上,且CD=CE,
分别在边AC,BC上,且CD=CE,
∴AC-CD=BC-CE,即AD=BE,点F、P、G分别为DE、DC、BC的中点,
∴PF=![]() AB,PG=
AB,PG=![]() CE,
CE,
∴PF=PG,
∵点F、P、G分别为DE、DC、BC的中点,
∴PG//BE,PF//AD,
∴∠PFB=∠A,∠DPG=∠DBC,
∴∠FPG=∠DPF+∠DPG
=∠PFB+∠DBA+∠DPG
=∠A+∠DBA+∠DBC
=∠A+∠ABC,
∵∠ABC+∠ACB=180°-∠C
∴∠FPG=180°-90°=90°,PF⊥PG;
(2)△FGP是等腰直角三角形
理由:由旋转知,∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△CAD≌△CBE(SAS),
∴∠CAD=∠CBE,AD=BE,
利用三角形的中位线得,PG=![]() BE,PF=
BE,PF=![]() AD,
AD,
∴PG=PF,
∴△FGP是等腰三角形,
利用三角形的中位线得,PG∥CE,
∴∠DPG=∠DBE,
利用三角形的中位线得,PF∥AD,
∴∠PFB=∠DAB,
∵∠DPF=∠DBA+∠PNB=∠DBA+∠DAB,
∴∠GPF=∠DPG+∠DPF=∠DBE+∠DBA+∠DAB
=∠ABE+∠DAB=∠CBA+∠CBE+∠DAB
=∠CBA+∠CAD+∠DAB=∠CBA+∠CAB,
∵∠ACB=90°,
∴∠CBA+∠CAB=90°,
∴∠GPF=90°,
∴△FGP是等腰直角三角形;
(3)由(2)知,△FGP是等腰直角三角形,PG=PF=![]() AD,
AD,
∴PG最大时,△FGP面积最大,
∴点D在AC的延长线上,
∴AD=AC+CD=11,
∴PG=![]() ,
,
∴S△PGF最大=![]() PG2=
PG2=![]()

 名校课堂系列答案
名校课堂系列答案