Question

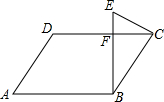
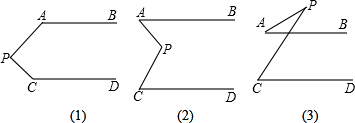
已知，AB∥CD，分别探讨三个图形中∠APC，∠PAB，∠PCD的关系．
（1）请说明图1，并加以证明．
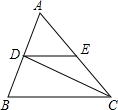
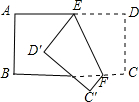
（2）猜想图2、图3中三个角的关系，不必说明理由

Answer 1

（1）如图1，过点P作PQ∥AB，
∵AB∥CD，
∴PQ∥AB∥CD，
∴∠PAB+∠1=180°，∠2+∠PCD=180°，
∵∠APC=∠1+∠2，
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°；


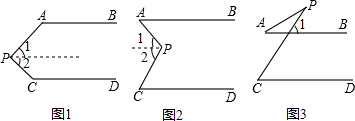
（2）如图2，过点P作PQ∥AB，
∵AB∥CD，
∴PQ∥AB∥CD，
∴∠1=∠PAB，∠2=∠PCD，
∵∠APC=∠1+∠2=∠PAB+∠PCD，
∴∠APC=∠PAB+∠PCD；
如图3，∵AB∥CD，
∴∠1=∠PCD，
∵∠1=∠PAB+∠APC，
∴∠PCD=∠PAB+∠APC．