��Ŀ����
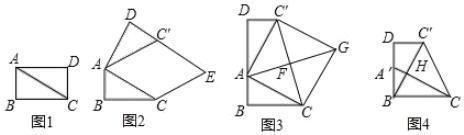
����Ŀ����ͼ1��E��������ABCD��AB�ϵ�һ�㣬����BD��DE������BDE�Ƶ�D��ʱ����ת90����ת��ǵ����߷ֱ�������BC���ڵ�F�͵�G��
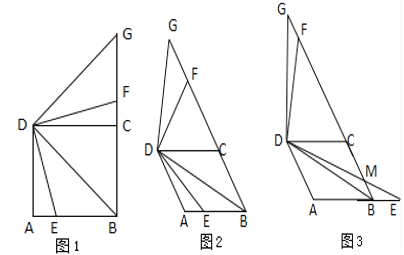
��1��̽���߶�BE��BF��DB֮���������ϵ��д�����۲�����֤����
��2�����ı���ABCDΪ���Σ���ADC=60����E������ABCD��AB����ֱ���ϵ�һ�㣬����BD��DE������BDE�Ƶ�D��ʱ����ת120����ת��ǵ����߷ֱ�������BC���ڵ�F�͵�G��
����ͼ2����E���߶�AB��ʱ����̽���߶�BE��BF��BD֮���������ϵ��д�����۲�����֤����
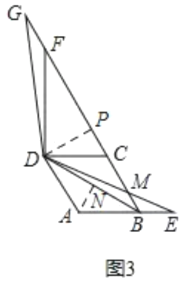
����ͼ3����E���߶�AB���ӳ�����ʱ��DE������BC�ڵ�M����BE=1��AB=2��ֱ��д���߶�GM�ij��ȣ�
���𰸡���1��![]() ��֤������������2����
��֤������������2����![]() ��֤������������
��֤������������![]()
��������
��1��������ת�����ʿ�֤�á�BDG�ǵ���ֱ�������Σ��õ�![]() ����֤����FDG�ա�EDB��ASA�����õ�FG=BE���ɵõ�
����֤����FDG�ա�EDB��ASA�����õ�FG=BE���ɵõ�![]() ��
��
��2���ٸ������ε������Լ���ת�����ʿɵá�DBG=��G=30�����Ӷ�֤����EDB�ա�FDG��ASA�����õ�BF+BE=BF+FG=BG������D��DP��BG�ڵ�P�����ù��ɶ��������������ε����ʵõ�BG=![]() ���Ӷ��ó�
���Ӷ��ó�![]() ���ɣ�
���ɣ�
�ڹ���A��AN��BD��BD�ڵ�N�����ݺ�30��ֱ�������ε����ʼ����������ε����ʣ�����BD��BF�ij�������ƽ���߷��߶γɱ��������ɵ�BM�ij��������߶εIJ�ɵý��ۣ�
�⣺��1��![]() ��
��
���ɣ�����ת��֪����BDE=��FDG����BDG=90����
���ı���ABCD�������Σ�
���CBD=45����
���G=45����
���G=��CBD=45����
��BD=DG��
��BDG�ǵ��������Σ�
��![]() ��
��
���ڡ�FDG���EDB�У�
��FDG=��EDB����G=��DBE=45����BD=DG��
���FDG�ա�EDB��ASA����
��FG=BE
��BE+BF=FG+BF=BG=![]() ��
��
��![]()
��2����![]()
���ɣ���ͼ2��������ABCD�У���ADB=��CDB=![]() ��ADC=30����
��ADC=30����
����ת120����֪����EDF=��BDG=120������EDB=��FDG��
�ڡ�DBG�У���G=180��-120��-30��=30����
���DBG=��G=30����
DB=DG��
���EDB�ա�FDG��ASA����
��BE=FD��
��BF+BE=BF+FG=BG��
����D��DP��BG�ڵ�P��
��BD=DG����BG=2BP��
�ߡ�DBC=30����
��DP=![]() ��
��
����Rt��BDP��![]() ��
��
��BG=![]()
��![]()
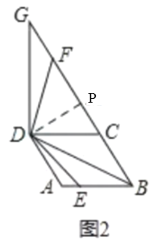
����ͼ3������A��AN��BD��BD�ڵ�N��
��Rt��ABN����ABN=30����AB=2��
��AN=1��BN=![]() ��
��
��BD=2BN=2![]() ��
��
��DC��BE��
��![]() ��
��
��CM+BM=2��
��BM=![]() ��
��
Rt��BDP����DBP=30����BD=2![]() ��
��
��BP=3
����ת�ã�BD=FD��
��BF=2BP=6��
��GM =BG-BM=6+1-![]() =
=![]() ��
��