题目内容
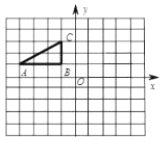
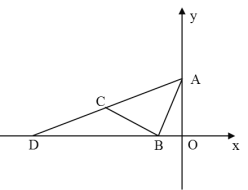
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() ,射线
,射线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是坐标平面内不同于点
是坐标平面内不同于点![]() 的一点,且以
的一点,且以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标;
的坐标;
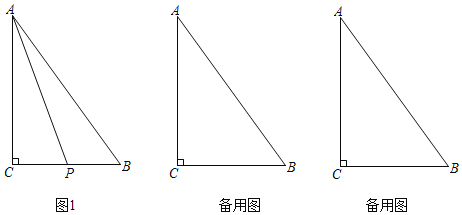
(3)点![]() 是线段
是线段![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,且
,且![]() 的面积等于
的面积等于![]() 面积的一半,求点
面积的一半,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)根据AB的解析式,求出点A、B的坐标,再求出AC的解析式,即可求出点D的坐标;
(2)以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,分三种情况,利用轴对称的性质进行讨论即可;
全等,分三种情况,利用轴对称的性质进行讨论即可;
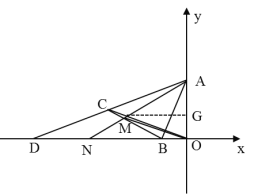
(3)求出BC的解析式,表示出点M的坐标,得出△AMG∽△ANO,表示出NO的长度,再根据“![]() 的面积等于
的面积等于![]() 面积的一半”,求出△OMN的面积,列出方程即可解答.
面积的一半”,求出△OMN的面积,列出方程即可解答.
(1)∵![]()
∴当y=0时,x=-1,当x=0时,y=2,
∴![]() ,
,![]()
设直线AC的解析式为y=kx+b,
将![]() ,
,![]() 代入得
代入得![]() ,解得:
,解得:![]()
∴直线AC解析式为:![]() ,
,
当y=0时,![]() ,解得:x=-6,
,解得:x=-6,
∴![]()
(2)①若△BPD≌△BCD,
则BP=BC,∠PBD=∠CBD,点P与点C关于x轴对称,
∴![]()
②当△DPB≌△BCD,且点P在x轴上方,
则DP=BC,∠PDB=∠CBD
∴P![]()
③当△DPB≌△BCD,且点P在x轴下方,
则DP=BC,∠PDB=∠CBD
则P![]()
∴![]() ,
,![]() ,
,![]()
(3)设BC的解析式为y=ax+c,则将![]() 与
与![]() 代入得:
代入得:
![]() ,解得:
,解得: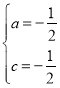 ,
,
∴![]()
设![]() ,其中
,其中![]() ,
,
过点M作MG⊥OA,
则△AMG∽△ANO
∵MG=-m,AG=![]()
∴![]() ,即
,即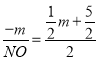
∴![]() ,
,
∵![]() ,
,
∴![]()
即![]() ,
,
解得:![]() 或
或![]() (舍去)
(舍去)
∴点![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
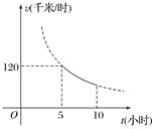
开心试卷期末冲刺100分系列答案【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)