题目内容
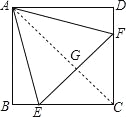
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④![]() .其中正确的个数为( )
.其中正确的个数为( )

A.1 B.2 C.3 D.4
【答案】C
【解析】
试题分析:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=![]() ,
,
设正方形的边长为a,
在Rt△ADF中,
a2+(a﹣![]() )2=4,
)2=4,
解得a=![]() ,
,
则a2=2+![]() ,
,
∴![]() =2+
=2+![]() ,
,
④说法正确,
∴正确的有①②④.
故选C.

练习册系列答案
相关题目
