题目内容
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA= ,则AD的长为( )
,则AD的长为( )

 ,则AD的长为( )
,则AD的长为( )
| A.2 | B. | C.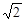 | D.1 |
A
首先根据题意画出图形,再作DE⊥AB于E,将AD构造为直角三角形的斜边,然后根据等腰直角三角形中斜边为直角边的
求解.
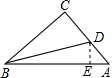
解:如图,作DE⊥AB于E.
∵tan∠DBA=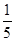 =
=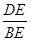 ,
,
∴BE=5DE.
∵△ABC为等腰直角三角形,
∴∠A=45°,
∴AE=DE.
∴BE=5AE,
又∵AC=6,
∴AB=6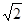 ,
,
∴AE+BE=AE+5AE=6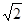 ,
,
∴AE=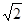 ,
,
∴在等腰直角△ADE中,由勾股定理,得AD=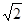
AE=2.
故选A.
本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解.
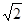
求解.

解:如图,作DE⊥AB于E.
∵tan∠DBA=
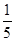 =
=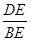 ,
,∴BE=5DE.
∵△ABC为等腰直角三角形,
∴∠A=45°,
∴AE=DE.
∴BE=5AE,
又∵AC=6,
∴AB=6
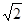 ,
,∴AE+BE=AE+5AE=6
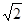 ,
,∴AE=
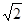 ,
,∴在等腰直角△ADE中,由勾股定理,得AD=
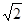
AE=2.
故选A.
本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解.

练习册系列答案
相关题目
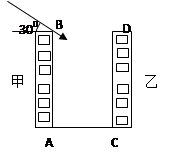

 0°方向,这时渔船改为向正东方向航行,问渔船有触礁有危险吗?为什么?
0°方向,这时渔船改为向正东方向航行,问渔船有触礁有危险吗?为什么?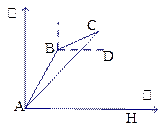
 中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.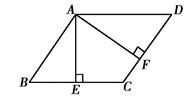
 ∠BAE=∠DAF;
∠BAE=∠DAF;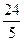 ,
,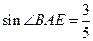 ,求CF的长.
,求CF的长. ,则菱形ABCD的周长是________.
,则菱形ABCD的周长是________.
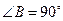 ,AB=BC=
,AB=BC= ,点D为BC的中点,求
,点D为BC的中点,求

