题目内容
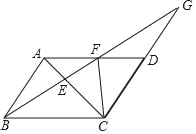
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为____
【答案】![]()
【解析】
先在Rt△BDC中,利用锐角三角函数求出BD,再利用直角三角形的性质求出DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.
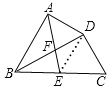
在Rt△BDC中,BC=4,∠DBC=30°,
∴cos∠DBC=cos30°![]()
∴BD=2![]() ,
,
连接DE,
∵∠BDC=90°,点E是BC中点,
∴DE=BE=CE=![]() BC=2,
BC=2,
∵∠DCB=30°,
∴∠BDE=∠DBC=30°,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠BDE,
∴DE∥AB,
∴△DEF∽△BAF,
∴![]() ,
,
在Rt△ABD中,∠ABD=30°,BD=2![]()
∴AB=3,
∴![]() ,
,
∴![]() ,
,
∴DF=![]() ,
,
故答案是:![]()

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目