��Ŀ����
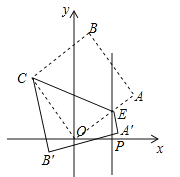
����Ŀ����֪����ͼ�ı���AOBCΪ�����Σ���C������Ϊ(4 ![]() ��0)������P��������OACB�ķ�����1����λÿ����ٶ������˶���ͬʱ��Q��������OBCA�ķ��������˶����ٶ���2����λ����ÿ�룬�˶�ʱ��Ϊt�룬����������ʱͬʱֹͣ�˶���
��0)������P��������OACB�ķ�����1����λÿ����ٶ������˶���ͬʱ��Q��������OBCA�ķ��������˶����ٶ���2����λ����ÿ�룬�˶�ʱ��Ϊt�룬����������ʱͬʱֹͣ�˶���
��1����A��������������AOBC������� ��
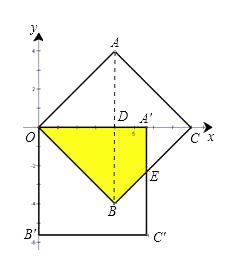
��2�����������Ƶ�O˳ʱ����ת45�㣬����ת�����������ԭ�����ε��ص����ֵ������
��3���˶�ʱ��tΪ������ʱ����A��P��B��Q�ĵ�Ϊ������ı���Ϊƽ���ı��Σ�
��4���Ƿ����������tֵ��ʹ��OPQ��Ϊ���������Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1����2![]() ,2
,2![]() ����16
����16
��2��
��OC=4![]() �ã�OA=OB=OC=AC=4��
�ã�OA=OB=OC=AC=4��
��ת��ɵ�OA��=OA=4��
��A��C=4![]() -4������֪��CA��E=90�㣬��OCB=45�㣬
-4������֪��CA��E=90�㣬��OCB=45�㣬
���A��EC�ǵ���ֱ�������Σ�
��A��E=A��C=4![]() -4��
-4��
��S�ı���OA��EB=S��OBC-S��A��EC=16![]() -16��
-16��
��3��
�⣺��P��OA��Q��OBʱ�������ڣ�
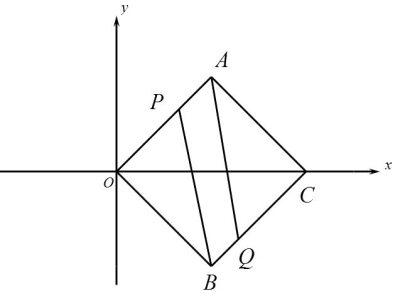
��P��OA��Q��BCʱ����AP=BQʱ������ΪAO//BC�����ı���APBQΪƽ���ı��Σ���ͼ��
AP=4-t,BQ =2t-4��
��4-t=2t-4,
���t=![]() .
.
����t=![]() ʱ���ı���APBQ��ƽ���ı���.
ʱ���ı���APBQ��ƽ���ı���.
��4��
���ڣ���Q����BC��ʱ��ʹOQ=QP��QMΪOP�Ĵ�ֱƽ���ߣ�
����OP=2OM=2BQ����OP=t��BQ=4-2t��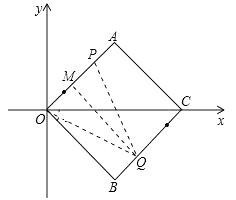
��t=2��4-2t����
��t=![]() .
.
����������1����������OACB�У�����AB����OC��D�㣬��OD=AD=![]() OC=2
OC=2![]() ,��A��2
,��A��2![]() ��2
��2![]() ��.
��.
����������![]() =16.
=16.
���Դ��ǣ���2![]() ��2
��2![]() ����16.
����16.
�����㾫����ͨ��������õ��������ε��ж���ƽ���ı��ε��ж����������һ������������������ȣ���ô�����������Եı�Ҳ��ȣ���ƣ��ȽǶԵȱߣ�������ж�����������֤��ͬһ���������еı���ȣ�����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı��μ����Խ����⣮

 ��У����ϵ�д�
��У����ϵ�д�