Question

【题目】已知，正方形ABCD，∠EAF＝45°，

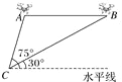
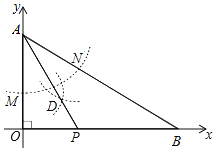
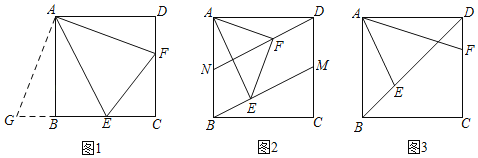
（1）如图1，当点E，F分别在边BC，CD上，连接EF，求证：EF＝BE+DF；

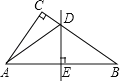
（2）如图2，点M，N分别在边AB，CD上，且BN＝DM，当点E，F分别在BM，DN上，连接EF，请探究线段EF，BE，DF之间满足的数量关系，并加以证明；

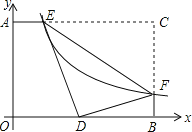
（3）如图3，当点E，F分别在对角线BD，边CD上，若FC＝2，则BE的长为　 　．

Answer 1

【答案】（1）见解析；（2）EF2＝BE2+DF2 ；理由见解析；（3）

【解析】

（1）如图1中，将△ADF绕点A顺时针旋转90°，得△ABG，想办法证明△EAG≌△EAF（SAS）．

（2）结论：EF2＝BE2+DF2，将△ADF绕点A顺时针旋转90°，得△ABH，（如图2）证明过程跟（1）类似，证得△EAH≌△EAF，把EF转化到EH，然后利用BN＝DM证明四边形BMDN为平行四边形得∠ABE＝∠FDM，得∠EBH＝∠ABH+∠ABE＝∠ADF+∠MDN＝90°，由EH2＝BE2+BH2得EF2＝BE2+DF2．

（3）作△ADF的外接圆⊙O，连接EF、EC，过点E分别作EM⊥CD于M，EN⊥BC于N（如图3）．想办法证明EF＝FC，即可推出封门村吗，证明EN＝CM即可．

（1）证明：如图1中，将△ADF绕点A顺时针旋转90°，得△ABG，

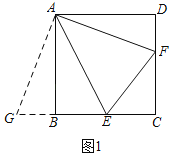
∴△ADF≌△ABG，

∴AF＝AG，DF＝BG，∠DAF＝∠BAG，

∵正方形ABCD，

∴∠D＝∠BAD＝∠ABE＝90°，AB＝AD，

∴∠ABG＝∠D＝90°，即G、B、C在同一直线上，

∵∠EAF＝45°，

∴∠DAF+∠BAE＝90°﹣45°＝45°，

∴∠EAG＝∠BAG+∠BAE＝∠DAF+∠BAE＝45°，

即∠EAG＝∠EAF，

∴△EAG≌△EAF（SAS），

∴EG＝EF，

∵BE+DF＝BE+BG＝EG，

∴EF＝BE+DF．

（2）结论：EF2＝BE2+DF2，

理由：将△ADF绕点A顺时针旋转90°，得△ABH，（如图2）

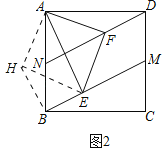
∴△ADF≌△ABH，

∴AF＝AH，DF＝BH，∠DAF＝∠BAH，∠ADF＝∠ABH，

∵∠EAF＝45°，

∴∠DAF+∠BAE＝90°﹣45°＝45°，

∴∠EAH＝∠BAH+∠BAE＝∠DAF+∠BAE＝45°，

即∠EAH＝∠EAF，

∴△EAH≌△EAF（SAS），

∴EH＝EF，

∵BN＝DM，BN∥DM，

∴四边形BMDN是平行四边形，

∴∠ABE＝∠MDN，

∴∠EBH＝∠ABH+∠ABE＝∠ADF+∠MDN＝∠ADM＝90°，

∴EH2＝BE2+BH2，

∴EF2＝BE2+DF2，

（3）作△ADF的外接圆⊙O，连接EF、EC，过点E分别作EM⊥CD于M，EN⊥BC于N（如图3）．

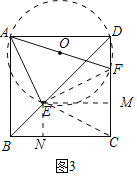
∵∠ADF＝90°，

∴AF为⊙O直径，

∵BD为正方形ABCD对角线，

∴∠EDF＝∠EAF＝45°，

∴点E在⊙O上，

∴∠AEF＝90°，

∴△AEF为等腰直角三角形，

∴AE＝EF，

∴△ABE≌△CBE（SAS），

∴AE＝CE，

∴CE＝EF，

∵EM⊥CF，CF＝2，

∴CM＝ CF＝1，

∵EN⊥BC，∠NCM＝90°，

∴四边形CMEN是矩形

∴EN＝CM＝1，

∵∠EBN＝45°，

∴BE＝EN＝ ．

故答案为：