题目内容
【题目】某商品经销店欲购进A、B两种纪念品，用160元购进的A种纪念品与用240元购进的B种纪念品的数量相同，每件B种纪念品的进价比A种纪念品的进价贵10元．
（1）求A、B两种纪念品每件的进价分别为多少元？
（2）若该商店A种纪念品每件售价24元，B种纪念品每件售价35元，这两种纪念品共购进1 000件，这两种纪念品全部售出后总获利不低于4 900元，求A种纪念品最多购进多少件．
【答案】
（1）解：设A种纪念品每件的进价为x元，则B种纪念品每件的进价（x+10）元，
由题意得： 
= 
，
解得：x=20，
经检验：x=20是原分式方程的解，
x+10=30，
答：A种纪念品每件的进价为20元，则B种纪念品每件的进价30元；
（2）解：设A种纪念品购进a件，由题意得：
（24﹣20）a+（35﹣30）（1000﹣a）≥4900，
解得：a≤100，
∵a为整数，
∴a的最大值为100．
答：A种纪念品最多购进100件．
【解析】（1）由“数量相同”，可用x的分式分别表示二者的数量，列出分式方程，检验，求出两种纪念品每件的进价；（2）“总获利不低于4 900元”列出不等式，求出a 的范围，此范围内求出整数的最大值.
【考点精析】通过灵活运用分式方程的应用，掌握列分式方程解应用题的步骤：审题、设未知数、找相等关系列方程、解方程并验根、写出答案（要有单位）即可以解答此题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
【题目】某校举办“红歌伴我成长”歌咏比赛活动，参赛同学的成绩分别绘制成频数分布表和频数分布直方图（均不完整）如图：
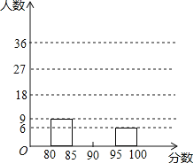
分数段 | 频数 | 频率 |
80≤x＜85 | 9 | 0.15 |
85≤x＜90 | m | 0.45 |
90≤x＜95 | ■ | ■ |
95≤x＜100 | 6 | n |
（1）求m，n的值分别是多少；
（2）请在图中补全频数分布直方图；
（3）比赛成绩的中位数落在哪个分数段？
