题目内容
【题目】如图，在菱形ABCD中，E，F分别在AB，CD上，且BE=DF，EF与BD相交于点O，连结AO．若∠CBD=35°，则∠DAO的度数为（ ）
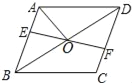
A. 35° B. 55° C. 65° D. 75°
【答案】B
【解析】试题分析：由菱形的性质以及已知条件可证明△BOE≌△DOF，所以可得BO=DO，即O为BD的中点，进而可得AO⊥BD，再由∠CBD=35°，则可以求出∠DAO的度数．
解：
∵四边形ABCD是菱形，
∴AB∥CD，
∴∠OEB=∠OFD，∠EBO=∠ODF，
∵BE=DF，
∴在△BOE和△DOF中，
，
∴△BOE≌△DOF，
∴BO=OD，
∴AO⊥BD，
∴∠AOD=90°，
∵∠CBD=35°，
∴∠ADO=35°，
∴∠DAO=55°，
故选B．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目