题目内容
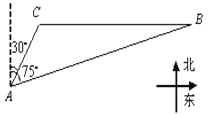
【题目】美丽的东昌湖赋于江北水城以灵性,周边景点密布。如图,A,B为湖滨的两个景点,C为湖心一个景点。景点B在景点C的正东,从景点![]() 看,景点B在北偏东
看,景点B在北偏东![]() 方向,景点C在北偏东
方向,景点C在北偏东![]() 方向。一游客自景点A驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到
方向。一游客自景点A驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到![]() 分钟)?
分钟)?
(参考数据sin![]() =0.97;cos
=0.97;cos![]() =0.26,tan
=0.26,tan![]() =3.73,
=3.73,![]() = 1.73)
= 1.73)
【答案】该游客自景点C驶向景点B约需27分钟.
【解析】分析:根据题意,过点A作AD垂直于直线BC,垂足为D,构造直角三角形,选择合适的三角函数进行解题求解即可.
详解:如图,过点A作AD垂直于直线BC,垂足为D,
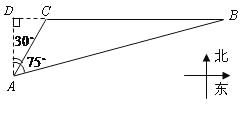
根据题意,得AC=20×10=200.
在Rt△ADC中,
AD=ACcos∠CAD=200cos30°=100![]() ,
,
DC=ACsin∠CAD=200sin30°=100.
在Rt△ADB中,
DB=ADtan∠BAD=100![]() tan75°.
tan75°.
∴CB=DB-DC=100![]() tan75°-100.
tan75°-100.
∴![]() =5
=5![]() tan75°-5≈27.
tan75°-5≈27.
即该游客自景点C驶向景点B约需27分钟.

【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹.下表是甲、乙两人各自的射击情况记录(其中乙的记录表上射中9,10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发).
甲
中靶环数(环) | 5 | 6 | 8 | 9 | 10 |
射中此环的子弹数(发) | 4 | 1 | 3 | 1 | 1 |
乙
中靶环数(环) | 5 | 6 | 7 | 9 | 10 |
射中此环的子弹数(发) | 2 | 3 | 2 |
(1)求甲同学在这次测验中平均每次射中的环数;
(2)从这次测验的平均成绩的角度考虑,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.
【题目】某班进行了一次数学測验,将成绩绘制成频数分布表和频数直方图的一部分如下:
成绩 | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
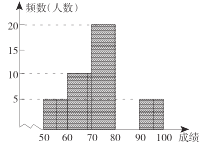
(1)在频数分布表中,![]() 的值为________,
的值为________,![]() 的值为________;
的值为________;
(2)将频数直方图补充完整;
(3)成绩在![]() 分以上(含
分以上(含![]() )的学生人数占全班总人数的百分比是多少?
)的学生人数占全班总人数的百分比是多少?