Question

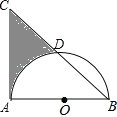
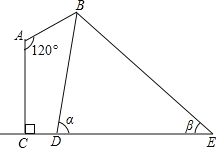
【题目】如图是某路灯在铅锤面内的示意图，灯柱AC的高为15.25米，灯杆AB与灯柱AC的夹角∠A＝120°，路灯采用锥形灯罩，在地面上的照射区域DE长为22米，从D、E两处测得路灯B的仰角分别为α和β，且tanα＝8，tanβ＝，求灯杆AB的长度．

Answer 1

【答案】灯杆AB的长度为1.5米.

【解析】

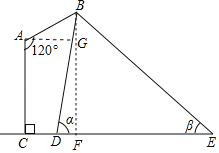
过点B作BF⊥CE，交CE于点F，过点A作AG⊥BF，交BF于点G，则FG=AC=15.25．设BF=4x知EF=5x、DF= ，由DE=22求得x，据此知BG=BF-GF，再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG．

解：过点B作BF⊥CE，交CE于点F，过点A作AG⊥BF，交BF于点G，则FG＝AC＝15.25．

由题意得∠BDE＝α，tan∠β＝．

设BF＝3x，则EF＝4x

在Rt△BDF中，∵tan∠BDF＝，

∴DF＝ ，

∵DE＝22，

∴x+5x＝22．

∴x＝4．

∴BF＝16，

∴BG＝BF﹣GF＝16﹣15.25＝0.75，

∵∠BAC＝120°，

∴∠BAG＝∠BAC﹣∠CAG＝120°﹣90°＝30°．

∴AB＝2BG＝1.5，

答：灯杆AB的长度为1.5米.