题目内容
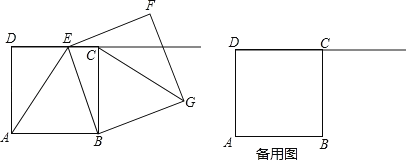
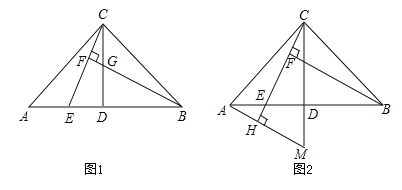
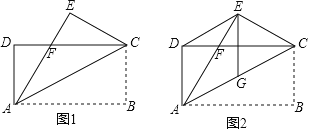
【题目】如图1,已知矩形ABCD,连接AC,将△ABC沿AC所在直线翻折,得到△AEC,AE交CD于点F.
(1)求证:DF=EF;
(2)如图2,若∠BAC=30°,点G是AC的中点,连接DE,EG,求证:四边形ADEG是菱形.
【答案】(1)证明见详解;(2)证明见详解.
【解析】
(1)根据矩形的性质得到AD=BC,∠D=∠B=90°,由折叠的性质得到∠E=∠B=90°,CE=BC.根据全等三角形的性质即可得到结论;
(2)根据折叠的性质得到∠AEC=∠B=90°,CE=BC,根据直角三角形的性质得到CE= ![]() AC,CE=AG=EG=AD,根据菱形的判定定理即可得到结论.
AC,CE=AG=EG=AD,根据菱形的判定定理即可得到结论.
解:(1)∵四边形ABCD是矩形,
∴AD=BC,∠D=∠B=90°.
∵将△ABC沿AC所在直线翻折,得到△AEC,
∴∠E=∠B=90°,CE=BC,
∴∠D=∠E,AD=CE.
∵∠AFD=∠CFE,
∴△ADF≌△CEF(AAS),
∴DF=EF;
(2)∵四边形ABCD是矩形,
∴AD=BC,∠ADC=∠B=90°.
∵将△ABC沿AC所在直线翻折,得到△AEC,
∴∠AEC=∠B=90°,CE=BC.
∵∠CAB=30°,
∴∠CAE=30°,
∴CE![]() AC.
AC.
∵点G是AC的中点,
∴CE=AG=EG=AD,
∴∠AEG=∠EAG=30°,
∴∠DAE=30°,
∴∠DAE=∠AEG,
∴AD∥GE,
∴四边形ADEG是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目