题目内容
【题目】如图，△ABC是等边三角形，D是BC延长线上一点，DE⊥AB于点E，EF⊥BC于点F．若CD=3AE，CF=6，则AC的长为_____．
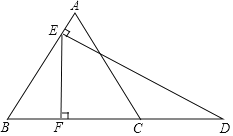
【答案】10
【解析】
利用“一锐角为30°的直角三角形中，30°所对的直角边等于斜边的一半”，通过等量代换可得.
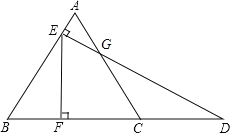
解： AC与DE相交于G，如图，
∵
为等边三角形，
∴AB=BC=AC，∠A=∠B=∠ACB=60°，
∵DE⊥AE，
∴∠AGE=30°，
∴∠CGD=30°，
∵∠ACB=∠CGD+∠D，
∴∠D=30°，
∴CG=CD，
设AE=x，则CD=3x，CG=3x，
在
中，AG=2AE=2x，
∴AB=BC=AC=5x，
∴BE=4x，BF=5x﹣6，
在
中，BE=2BF，
即4x=2（5x﹣6），解得x=2，
∴AC=5x=10．
故答案为10．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
