Question

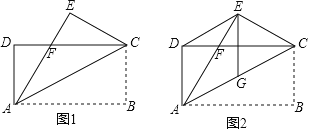
【题目】如图，已知正方形ABCD，AB=8，点E是射线DC上一个动点(点E与点D不重合)，连接AE，BE，以BE为边在线段AD的右侧作正方形BEFG，连结CG．

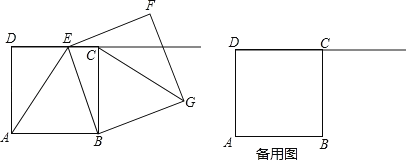
（1）当点E在线段DC上时，求证：△BAE≌△BCG；

（2）在（1）的条件下，若CE=2，求CG的长；

（3）连接CF，当△CFG为等腰三角形时，求DE的长．

Answer 1

【答案】（1）证明见解析；（2）CG=10；（3）当△CFG为等腰三角形时，DE的长为4或8或16．

【解析】

(1)由正方形的性质得出，AB=BC，BE=BG，∠ABC=∠EBG=90°，易证∠ABE=∠CBG，由SAS证得△BAE≌△BCG；
(2)由△BAE≌△BCG，得出AE=CG，DE=CDCE=6，由勾股定理得出，即可得出结果；
(3)①当CG=FG时，易证AE=BE，由HL证得Rt△ADE≌Rt△BCE，得出DE=CE= DC=4；
②当CF=FG时，点E与点C重合，DE=CD=8；
③当CF=CG时，点E与点D重合时，DE=0；
④当CF=CG，点E在DC延长线上时，DE=16．

（1）证明∵四边形ABCD和四边形BEFG都是正方形，

∴AB=BC，BE=BG，∠ABC=∠EBG=90°，

∴∠ABC﹣∠EBC=∠EBG﹣∠EBC，即∠ABE=∠CBG，

在△BAE和△BCG中，，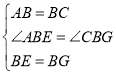

∴△BAE≌△BCG(SAS)；

（2）解：∵△BAE≌△BCG，

∴AE=CG．

∵四边形ABCD正方形，

∴AB=AD=CD=8，∠D=90°，

∴DE=CD﹣CE=8﹣2=6，

∴AE10，

∴CG=10；

（3）解：①当CG=FG时，如图1所示：

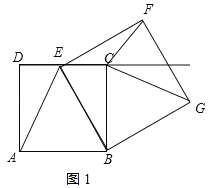
∵△BAE≌△BCG，

∴AE=CG．

∵四边形BEFG是正方形，

∴FG=BE，

∴AE=BE，

在Rt△ADE和Rt△BCE中，，

∴Rt△ADE≌Rt△BCE(HL)，

∴DE=CEDC8=4；

②当CF=FG时，如图2所示：

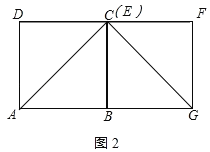
点E与点C重合，即正方形ABCD和正方形BEFG的一条边重合，DE=CD=8；

③当CF=CG时，如图3所示：

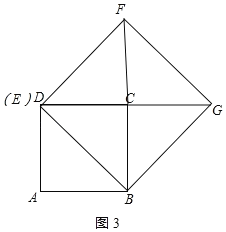
点E与点D重合，DE=0；

∵点E与点D不重合，

∴不存在这种情况；

④CF=CG，当点E在DC延长线上时，如图4所示：

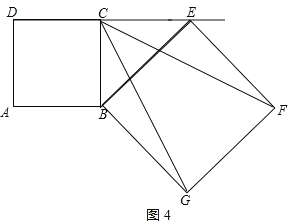
DE=CD+CE=16；

综上所述：当△CFG为等腰三角形时，DE的长为4或8或16．