题目内容
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
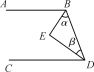
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
【答案】见解析.
【解析】
理解题意,分析每一步的推导根据.由角的平分线定义得∠ABD=2∠α,∠BDC=2∠β,
根据等量代换得∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β),由已知∠α+∠β=90°,再由等量代换得∠ABD+∠BDC=180°,最后根据“同旁内角互补两直线平行”得AB∥CD.
BE平分∠ABD(已知),
∴∠ABD=2∠α(角平分线的定义).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (角平分线的定义)
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换)
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(等量代换).
∴AB∥CD(同旁内角互补两直线平行).
故答案为:角平分线的定义,角平分线的定义,等量代换,等量代换,同旁内角互补两直线平行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目