题目内容
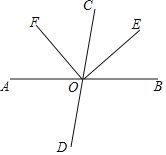
【题目】如图,直线AB,CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF⊥OE.
(1)求∠COF的度数;
(2)说明OF平分∠AOC.
【答案】(1)50°;(2)见解析
【解析】
(1)依据∠BOC=80°,OE是∠BOC的角平分线,即可得到∠COE=![]() ∠BOC=40°,再根据OF⊥OE,即可得到∠COF=90°﹣∠COE=50°;
∠BOC=40°,再根据OF⊥OE,即可得到∠COF=90°﹣∠COE=50°;
(2)依据∠BOC=80°,得到∠AOC=100°,再根据∠COF=50°,即可得到∠COF=![]() ∠AOC,据此可得OF平分∠AOC.
∠AOC,据此可得OF平分∠AOC.
解:(1)∵∠BOC=80°,OE是∠BOC的角平分线,
∴∠COE=![]() ∠BOC=40°,
∠BOC=40°,
又∵OF⊥OE,
∴∠COF=90°﹣∠COE=50°;
(2)∵∠BOC=80°,
∴∠AOC=100°,
又∵∠COF=50°,
∴∠COF=![]() ∠AOC,
∠AOC,
∴OF平分∠AOC.

练习册系列答案
相关题目