题目内容
【题目】已知等腰三角形ABC,AD为BC边上的高线,且有![]() ,AC上有一点E,并且满足AE:EC=2:3,则tan∠ADE的值是__.
,AC上有一点E,并且满足AE:EC=2:3,则tan∠ADE的值是__.
【答案】![]() 或
或![]() 或
或![]() .
.
【解析】
分三种情况进行讨论:①如果AB=AC,过E点作CD的平行线交AD于F.②如果BA=BC,过E点作CD的平行线交AD于F.③如果CA=CB,过E点作CD的平行线交AD于F,作CG⊥AB于G.利用锐角三角函数的定义、平行线分线段成比例定理可求出∠ADE的正切值.
分三种情况:
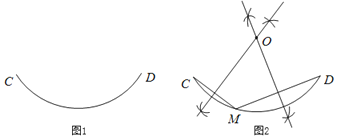
①如果AB=AC,过E点作CD的平行线交AD于F.如图1.
∵AD为BC边上的高线,tan∠B=![]() ,
,
∴EF⊥AD,tan∠C=![]() .
.
设AE=2a,
∵AE:CE=2:3,
∴CE=3a,AC=5a.
∵tan∠C=![]() ,
,
∴sin∠C=![]() ,cos∠C=
,cos∠C=![]() .
.
在直角△ADC中,AD=AC·sin∠C=5a×![]() =3a.
=3a.
在直角△AFE中,AF=AE·sin∠AEF=AE·sin∠C=2a×![]() =
=![]() a.
a.
EF=AE·cos∠AEF=AE·cos∠C=2a×![]() =
=![]() a.
a.
DF=AD﹣AF=3a﹣![]() a=
a=![]() a.
a.
在直角△DFE中,tan∠ADE=![]() =
=![]() =
=![]() ;
;
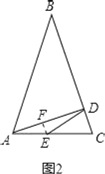
②如果BA=BC,过E点作CD的平行线交AD于F.如图2.
∵AD为BC边上的高线,tan∠B=![]() =
=![]() ,
,
∴可设AD=3k,则BD=4k,
由勾股定理得AB=5k,
∴BC=AB=5k,DC=AC﹣BD=k.
∵EF∥CD,AE:EC=2:3,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AF=![]() k,EF=
k,EF=![]() k,
k,
∴DF=AD﹣AF=3k﹣![]() k=
k=![]() k.
k.
在直角△DFE中,tan∠ADE=![]() =
=![]() =
=![]() ;
;
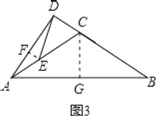
③如果CA=CB,过E点作CD的平行线交AD于F,作CG⊥AB于G.如图2.
∵在直角△BCG中,tan∠B=![]() =
=![]() ,
,
∴可设CG=3b,则BG=4b,AB=2BG=8b,
由勾股定理得BC=5b,则AC=BC=5b,
∵AE:EC=2:3,
∴AE=2b,EC=3b.
∵在直角△ABD中,tan∠B=![]() =
=![]() ,AB=8b,
,AB=8b,
∴AD=![]() ×8b=
×8b=![]() b,BD=
b,BD=![]() ×8b=
×8b=![]() b,
b,
∴CD=BD﹣BC=![]() b﹣5b=
b﹣5b=![]() b.
b.
∵EF∥CD,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AF=![]() b,EF=
b,EF=![]() b,
b,
∴DF=AD﹣AF=![]() b﹣
b﹣![]() b=
b=![]() b.
b.
在直角△DFE中,tan∠ADE=![]() =
=![]() =
=![]() .
.
故答案为![]() 或
或![]() 或
或![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
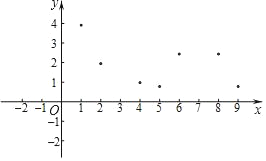
x | … | 1 | 2 | 4 | 5 | 6 | 8 | 9 | … |
y | … | 3.92 | 1.95 | 0.98 | 0.78 | 2.44 | 2.44 | 0.78 | … |
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=7对应的函数值y约为多少;
②写出该函数的一条性质.